簡介
在數學和程式設計中， 平方求冪（英語：exponentiating by squaring）或 快速冪是快速計算一個數（或更一般地說，一個半群的元素，如多項式或方陣）的大正整數冪的一般方法。這些算法可以非常通用，例如用在模算數或矩陣冪。對於通常使用加性表示法的半群，如密碼學中使用的橢圓曲線，這種方法也稱為 double-and-add。
基本方法
該方法是基於觀察到，對於正整數n，我們有
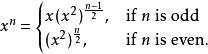平方求冪該方法使用指數的位（二進制的位，即bit，下文稱為“位”）來確定計算哪些冪。
此例顯示如何使用此方法計算{\displaystyle x^{13}}。 冪指數13的二進制為1101。這些位按照從左到右的順序使用。 指數有4位，所以有4次疊代。
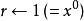平方求冪首先，將結果初始化為1：
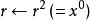平方求冪
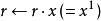平方求冪，第1位 = 1，所以計算。
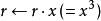平方求冪
平方求冪，第2位 = 1，所以計算。
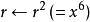平方求冪，第3位 = 0，所以這一步我們什麼都不做。
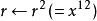平方求冪
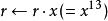平方求冪，第4位 = 1，所以計算。
替代方法及推廣
主條目：加法鏈求冪
平方求冪可以看作是一個次優的加法鏈求冪算法：它通過由重複指數加倍（平方）和指數遞增（乘以 x）組成的加法鏈來計算指數。更一般地，如果允許 任何先前計算的指數相加（通過乘以 x的冪），有時可以讓求冪運算的乘法次數更少（但通常使用更多的記憶體）。 n=15 時的最少次數：
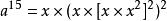平方求冪（平方求冪，6次乘法）
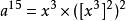平方求冪（最優加法鏈，在復用 x的情況下只需要5次乘法）
一般來說，求給定指數的最佳加法鏈是一個難題，因為沒有已知的高效算法，所以最優鏈通常只用於小指數（比如，在編譯器中已經預先存儲了小指數冪的最佳鏈）。不過，有一些啟發式算法，雖然不是最優的，但是由於額外的簿記工作和記憶體使用量的增加而導致的乘法次數少於平方求冪。無論如何，乘法的次數永遠不會比Θ(log n) 增長得更慢，所以這些算法只能減小平方求冪的漸進複雜度的常數因子。
參見
•模冪運算
•向量加法鏈
•蒙哥馬利算法
•非相鄰形式
•加法鏈
