簡介
常數變易公式是常微分方程的常數變易法線上性泛函微分方程的推廣。在拉普拉斯變換表示之下，由通解同樣可以得出常數變易公式。
常數變易公式設齊次線性與非齊次泛函微分方程ẋ(t)=L(t,x)，ẋ(t)=L(t,x)+f(t)，過(σ,φ)∈R×C的解整體存在，記x(t,σ,φ)為ẋ(t)=L(t,x)的解，x(t,σ,φ,f)為ẋ(t)=L(t,x)+f(t)的解，則有當t≥σ時幾乎處處成立，並稱為常數變易公式。
具體內容
常數變易公式
常數變易公式
常數變易公式常數變易公式中U(t,s)滿足方程U(t,s)稱為基解陣。
若L(t,x) =ax(t) +bx(t-τ) ,則U(t,s)=X(t-s)，X(t-s)是由拉普拉斯變換表示的基礎解。對中立型泛函微分方程類似地可以給出公式。
常數變易法
常數變易法是個特殊的變數代換法。
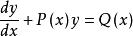常數變易公式
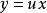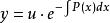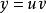常數變易公式
常數變易公式
常數變易公式
常數變易公式
常數變易公式
常數變易公式 常數變易公式 常數變易公式 常數變易公式 常數變易公式 常數變易公式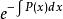
常數變易公式 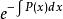常數變易公式
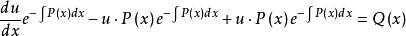常數變易公式
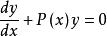常數變易公式對於一階線性微分方程，在解齊次方程時用代換，而這裡是; 一般地代換，為的確定函式，是的未知函式，那么乘以可以表示任意的的函式。選一個適當的，就能使方程化成變數可分離的。這個是怎么選定的，反向過來看，把帶入後，得到，剛好後兩項相互抵消，就可分離變數。其實這個問題就是解, 剛好就是求對應的齊次方程的解。
