引示例
示例：已知X、Y，X-Y=8,且X是Y的3倍,求X、Y。
解答：Y=8÷（3-1）=4；X=4×3=12。
公式
差÷（倍數－1）=小數；
小數+差
或
小數×倍數=大數。
例題
1、兩根電線長度相差30米，長的那根是短的那根的4倍。這兩根電線各長多少米？
分析與解答：這題的“差”=30，倍數=4，由差倍公式得
短的電線長：30÷(4－1)=10(米)，
長的電線長：10+30=40(米)或10×4=40(米)。
答：短的電線長10米，長的電線長40米。
2、甲、乙二工程隊，甲隊有56人，乙隊有34人。兩隊調走同樣多人後，甲隊人數是乙隊人數的3倍。問：調動後兩隊各有多少人？
分析：“1倍”數是乙隊調動後剩下的人數。因甲、乙隊調走的人數相同(不影響他們二隊人數之差)，所以，甲、乙兩隊人數之差仍是56－34=22(人)。
解：由差倍公式得調動後乙隊有
(56－34)÷(3－1)=11(人)。
調動後甲隊有：
11×3=33(人)或11+(56－34)=33(人)。
答：調動後甲隊有33人，乙隊有11人。
3、甲、乙兩桶油重量相等。甲桶取走26千克油，乙桶加入14千克油，這時，乙桶油的重量是甲桶油的重量的3倍。兩桶油原來各有多少千克？
分析與解答：當甲桶取走26千克、乙桶加入14千克後，乙桶里的油就是甲桶里的油的3倍，所以，“1倍”數是甲桶里剩下的油，差是26+14=40(千克)。由差倍公式知，
“1倍”數=(26+14)÷(3－1)=20(千克)。
故甲、乙桶原來各有油：20+26=46(千克)，
或20×3－14=46(千克)。
答：原來各有46千克。
4、小雲比小雨少20本書，後來小雲丟了5本書，小雨新買了11本書，這時小雨的書比小雲的書多2倍。問：原來兩人各有多少本書？
分析與解：“小雨的書比小雲的書多2倍”，即小雨的書是小雲的書的3倍。這個“倍數”是變化後的，所以“1倍”數應是小雲變化後的書。“差”是20+5+11=36(本)。
根據差倍公式得：
小雲現有書
(20+5+11)÷(3－1)=18(本)。
小雲原來有書18+5=23(本)，
小雨原來有書23+20=43(本)。
答：原來小雲有23本書，小雨有43本書。
5、李師傅生產的零件個數是徒弟的6倍，如果兩個人各再生產20個，那么李師傅生產零件的個數是徒弟的4倍，兩人原來各生產零件多少個？
應該這么想，徒弟是1份，師傅是6份。這是6倍關係。
徒弟是1份+20，師傅是6份+20。這是4倍關係。
在4倍關係中，師傅比徒弟多多少，應該是（6份+20）-（1份+20）=原來的5份。也是現在的3份。
現在的3份=（原來的1份+20）*3
=原來的3份+60
再和原來的5份一比，60個零件是2份，
30個零件是1份。
李師傅生產的零件180個，徒弟是30個。
6、某班買來單價為0.5元的練習本若干，如果將這些練習本只給女生，平均每人可得15本；如果將這些練習本只給男生，平均每人可得10本。那么，將這些練習本平均分給全班同學，每人應付多少錢?
男生，平均每人可得10本,這兩句話說男生多。
女生每人交15*0.5=7.5元
男生每人交10*0.5=5.0元
根據15 10，可得男女比例為 3：2。 女生占 2/5 ，男生占3/5。
[7.5*3/5+5.0*2/5]/1=6元
這些練習本平均分給全班同學，每人應付6元
很遺憾，以上計算是錯誤的
根據15，10，得出男女生比例是15：10.假設男生為15份，女生為10份。則總本數為15×10=150
0.5×150÷（15+10）=3元。正確答案為3元。
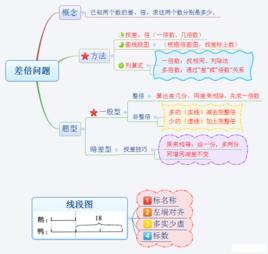
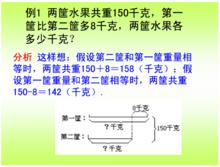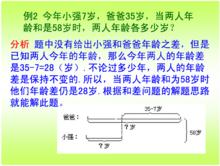差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題
差倍問題：
