基本定義
（1）工期最佳化是壓縮計算工期，以達到要求工期目標，或在一定約束條件下使工期最短的過程。
（2）工期最佳化一般通過壓縮關鍵工作的持續時間來達到最佳化目標。
（3）在最佳化過程中，要注意不能將關鍵工作壓縮成非關鍵工作，但關鍵工作可以不經壓縮而變成非關鍵工作。
（4）在最佳化過程中，當出現多條關鍵線路時，必須將各條關鍵線路的持續時間壓縮同一數值。否則，不能有效地將工期縮短。
最佳化方法
（1）找出網路計畫中的關鍵線路並求出計算工期。一般可用標號法確定出關鍵線路及計算工期。
（2）按要求工期計算應縮短的時間（ΔT）。應縮短的時間等於計算工期與要求工期之差。即
Δ T = T c − T r
（3）選擇應優先縮短持續時間的關鍵工作（或一組關鍵工作）。選擇時應考慮下列因素：
1）縮短持續時間對質量和安全影響不大的工作；
2）有充足備用資源的工作；
3）縮短持續時間所需增加的費用最少的工作。
（4）將應優先縮短的關鍵工作壓縮至最短持續時間，並找出關鍵線路。若被壓縮的關鍵工作變成了非關鍵工作，則應將其持續時間再適當延長，使之仍為關鍵工作。
（5）若計算工期仍超過要求工期，則重複以上步驟，直到滿足工期要求或工期已不能再縮短為止。
（6）當所有關鍵工作或部分關鍵工作已達最短持續時間而尋求不到繼續壓縮工期的方案但工期仍不能滿足要求工期時，應對計畫的原技術、組織方案進行調整，或對要求工期重新審定。
步驟和方法
工期最佳化的步驟和方法
（1）找出網路計畫中的關鍵線路並求出計算工期。一般可用標號法確定出關鍵線路及計算工期。
（2）按要求工期計算應縮短的時間（ΔT）。應縮短的時間等於計算工期與要求工期之差。即 ΔT = Tc − Tr
（3）選擇應優先縮短持續時間的關鍵工作（或一組關鍵工作）。
選擇時應考慮下列因素：
1）縮短持續時間對質量和安全影響不大的工作；
2）有充足備用資源的工作；
3）縮短持續時間所需增加的費用最少的工作。
（4）將應優先縮短的關鍵工作壓縮至最短持續時間，並找出關鍵線路。若被壓縮的關鍵工作變成了非關鍵工作，則應將其持續時間再適當延長，使之仍為關鍵工作。
（5）若計算工期仍超過要求工期，則重複以上步驟，直到滿足工期要求或工期已不能再縮短為止。
（6）當所有關鍵工作或部分關鍵工作已達最短持續時間而尋求不到繼續壓縮工期的方案但工期仍不能滿足要求工期時，應對計畫的原技術、組織方案進行調整，或對要求工期重新審定。
實例
例如，已知網路計畫如圖-1所示，
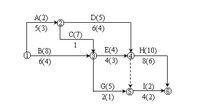工期最佳化圖1 某網路計畫圖
圖中箭線下方為正常持續時間和括弧內為最短持續時間，箭線上方括弧內為優選係數，優先係數愈小愈應優先選擇，若同時縮短多個關鍵工作，則該多個關鍵工作的優先係數之和（稱為組合優選係數）最小者亦應優先選擇。設要求工期為15天，試對其進行工期最佳化。
解：（1）用標號法求出正常持續時間下的計算工期和關鍵線路。如圖-2所示。
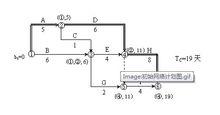工期最佳化圖2 初始網路計畫圖
（2）應縮短時間：Δ T = T c − T r = 19 − 15 = 4天。
（3）應優先縮短優選係數小的關鍵工作A的持續時間。
（4）將關鍵工作A壓至最短持續時間3天，用標號法求出關鍵線路，如圖-3所示。
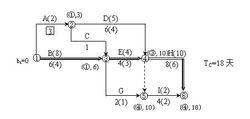工期最佳化圖3 A縮短至最短持續時間的網路計畫
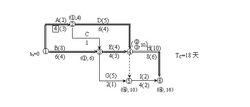
此時關鍵工作A壓縮後成了非關鍵工作，說明有無效壓縮，故需將其鬆弛，使之仍成為關鍵工作。現將其鬆弛至4天，找出關鍵線路如圖-4，
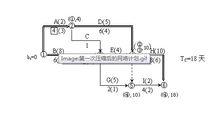工期最佳化圖4 第一次壓縮後的網路計畫
此時A成了關鍵工作。圖中有兩條關鍵線路，即ADH和BEH。此時計算工期
T c = 18天，Δ T1 = 18 − 15 = 3天。
（5）由於計算工期仍大於要求工期，故需繼續壓縮。如圖-4所示，有五個壓縮方案：
工期最佳化圖4 第一次壓縮後的網路計畫
1）壓工作A、B，組合優選係數為2+8=10；
2）壓工作A、E，組合優選係數為2+4=6；3）壓工作D、E，組合優選係數為 5+4=9；4）壓工作D、B，組合優選係數為5+8=13；5）壓工作H，優選係數為10。決定壓縮優選係數最小者，即壓工作A、E。這兩個工作均壓縮至最短持續時間3天。用標號法找出關鍵線路和計算工期，如圖-5所示。
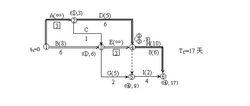工期最佳化圖5 第二次壓縮後的網路計畫
此時關鍵線路仍為ADH和BEH。計算工期 T c = 17天，Δ T2 = 17 − 15 = 2天。
由於工作A和E已達最短持續時間，不能再壓縮，可假定它們的優選係數為無窮大。
（6）由於計算工期仍大於要求工期，故需繼續壓縮。在前述的五個壓縮方案中，前三個方案的優選係數已變為無窮大，現只有壓工作B、D方案，優選係數為13；壓工作H方案，優選係數為10。故採取壓縮工作H的方案，將工作H壓縮2天。則計算工期 天，等於要求工期的最佳化方案，如圖-6所示 。
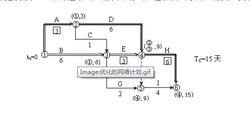工期最佳化圖6 最佳化的網路計畫
