簡介
材料在單向拉伸(或壓縮)過程中,由於加工硬化,塑性流動所需的應力值隨變形量增大而增大。對應於變形過程某一瞬時進行塑性流動所需的真實應力叫做該瞬時的屈服應力(Y),亦稱流動應力。如果忽略材料的加工硬化,可以認為屈服應力為一常數,並近似等於屈服極限(σs)。實際上,屈服應力是一個由形變速度、形變溫度、形變程度決定的函式,且這些參數彼此相互影響,並通常與材料特性相關。
計算單向拉伸的屈服應力通常可以從應力矢量中求得,有兩種假說理論,Tresca和Von Mises,都是以發明人的姓氏命名的。
反載軟化現象
在塑性變形階段,實際應力曲線上每一點的應力值,都可理解為材料在相應的變形程度下的屈服點。
如果卸載後反向載入,由拉伸改為壓縮,應力與應變的關係又會產生什麼樣的變化呢?試驗表明,反向載入時,材料的屈服應力較拉伸時的屈服應力有所降低,出現所謂反載軟化現象。反向載入時屈服應力的降低量,視材料的種類及正向載入的變形程度不同而異。關於反載軟化現象,有人認為可能是因為正向載入時材料中的殘餘應力引起的。
結構屈服應力的求法,一般借用前期固結壓力求結構屈服應力,其主要方法有:Casagrande法和Schmertman法等方法。
屈服應力的確定方法
在金屬的彈性變形達到極限後,其強度就會發生小範圍的波動,這時也就是塑性變形開始了。這個點即是屈服點,這時所受的應力就叫做屈服應力或屈服強度。屈服點之前一般金屬的變形量與拉力接近一次線性關係,屈服點之後就變為二次線性關係(拋物線),即拉力增加不大,但產生的變形量卻相對較大。
 屈服應力
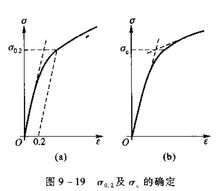
屈服應力對於多晶體材料而言,材料塑性變形的屈服應力一般取殘餘應變為0.2%時所加的應力,即所謂的σ0.2,如圖(a)所示。另一種方法是把應力-應變曲線的彈性階段及塑性階段曲線外推的交點作為屈服應力,如圖(b)所示。
有些鋼材(如高碳鋼)無明顯的屈服現象,通常以發生微量的塑性變形(0.2%)時的應力作為該鋼材的屈服強度,稱為條件屈服強度。
