簡介
對稱導數是導數的一種推廣。
對稱導數常特指二階對稱導數,它是黎曼(Riceman,(G.F.)B.)於1854年研究三角級數時首先引進的,後來由施瓦茲(Schwarz,H.A.)詳細研究過,故又稱為黎曼導數或施瓦茲對稱導數。
舉例
設一元函式f在x附近有定義,f在x處的:
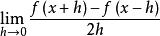 對稱導數
對稱導數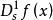 對稱導數
對稱導數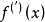 對稱導數
對稱導數一階對稱導數是數 ,記為 或 ;
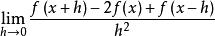 對稱導數
對稱導數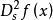 對稱導數
對稱導數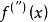 對稱導數
對稱導數二階對稱導數是數 ,記為 或 。
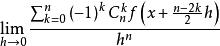 對稱導數
對稱導數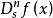 對稱導數
對稱導數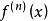 對稱導數
對稱導數n階對稱導數為 ,記為 或 。
對稱差
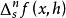 對稱導數
對稱導數n階對稱導數分式中的分子記為 ,稱為f在x處的n階對稱差。記號中的s是symmetric(對稱)的第一個字母。
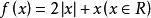 對稱導數
對稱導數f可微時,f存在且等於f',反之不然,如 ,當f與f均連續時f可微。
