對流擴散問題概述
對流擴散問題,主要研究流體中由流體質點所攜帶的某種物理量,如溫度或溶解於流體中的物質的濃度在流動過程中的變化規律。這種變化一般包括對流、擴散以及由於某種物理化學原因引起的物理量自身衰減或增長的過程。
對流擴散現象包括河流污染、大氣污染、核廢物污染中污染物質的分布,流體的流動和流體中熱的傳導等眾多物理現象。對於同時伴有物質輸運和分子擴散的物理過程以及粘性流體的流動,其數學模型通常為對流擴散方程或含有此類方程的偏微分方程組的定解問題。
對流擴散問題涉及的物理過程
假定u =u (x ,y ,z ,t)是流體中單位體積所攜帶的物理量。如物理量是流體介質的質量,則u表示密度;如物理量是某種污染物的含量,則u是表示污染濃度;如物理量是熱能,則u是熱量或溫度。為研究物理量u的變化規律,在流場中任取一個有限區域V,其邊界為S。V中流體所攜帶的物理量u的變化,由下列三方面物理過程組成。
(1)對流過程
由於流體處於巨觀的流動狀態,V中u的總量因對流而發生變化,可以認為它由兩方面組成:一項是在u中V隨著
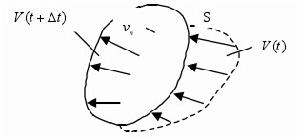
(2)擴散過程
擴散過程包含有分子布朗運動形成的分子擴散以及流體湍流運動形成的湍流擴散。這種擴散使得物理量u在流場中由高值向低值方向移動。若擴散的速率用q表示,它是單位時間內通過單位面積的物理量,Fick定律給出了物理量在流場中的擴散速率公式q=-Kgrad(u),其中張量K=Km+Kt,Km是分子擴散係數張量,Kt是湍流擴散係數張量。K的各個分量值取決於含有物理量u的流體的狀態與性質。一般地說,企圖在理論在確定K值是非常困難的,通常是通過實驗測定。如果擴散是各向同性的,則可寫成q=-kgrad(u),其中k是擴散係數,它可以是u或其它物理量的函式,也可以是常數。
(3)源和匯
流場中物理量u的自身增長與衰減,一般是通過分布在流場中的源和匯來描述。這種源和匯是場的分布函式,記為Q。Q>0表示源,它將使u增長;Q<0表示匯,它將使u減小。u增長或減小的速率由源或匯的強度,即Q絕對值的大小來反映。在區域V中,由於源匯的作用使u的增加量為∮‍QdV,通常我們將Q分為源增長項和匯衰減項。線性衰減類型的表達式為Q =f-βu,其中f>0是源分布函式,β≥0是衰減函式。另一種常用的衰減類型的時間的指數規律,Q =f-u0 e^(-1/γ),其中u0是初始時刻物理量u的濃度,t是時間變數,γ是衰減常數。
對流擴散問題的難點
對流擴散方程右端第一項為擴散項,左端第二項則是對流項。由於其方程本身的特點,給建立準確有效的數值求解方法帶來一定的困難。對流和擴散給流體中由流體攜帶的某種物理量的變化過程,可以通過一個無量綱的特徵參數(Peclet數)來描述,Peclet數Pe的定義為:Pe=|ν‍|L/D。這裡v是來流速度,L是特徵長度,D是物質的擴散係數。如果Pe數較小,即對流效應相對較弱,這類問題中,擴散占主導地位,方程是橢圓型或拋物線型;如果Pe數較大,即溶質分子的擴散相對於流體速度而言是緩慢的,這類問題中,對流占優,方程具有雙曲型方程的特點。
對於對流占優問題,用通常的差分法或有限元法進行求解將出現數值震盪。為了避免求解結果產生數值振盪,獲得穩定解,則應使每個單元的局部Peclet數,Peh=|ν‍|h/D≤‍2,這裡h為單元的最大尺寸,|v|為單元中的最大速度分量值。因此,用本文方法求解對流占優對流擴散問題,要得到穩定解,則要通過加密有限元格線來實現。
