乘法的基本規律
首先看一下十進制數的乘法。為了方便起見,假定十進制數的各位要么為 1要么為0,例如 (1000) ×(1001) :
從上面的步驟我們可以看到:
(1)從右到左用乘數的每一位乘以被乘數,每一次乘得的中間結果比上一次的結果往左移一位。
(2)積的位數比被乘數和乘數的位數要多得多。因此,乘法必須像加法那樣處理溢出問題,如果兩個32 位的數相乘,積也只有32 位的時候,就會出現溢出。在上面的例子中,我們把十進制數的各位限制為0 或1。因此,每一步的乘法相當簡單:
(1) 如果乘數位是 1,則簡單的複製被乘數到合適的位置(ix 被乘數);
(2) 如果乘數位是 0,則在合適的位置置0
因為二進制數的各位是0 或1,所以與上面情況類似。
既然已經知道了乘法的基本規律,下一步就是設計高度最佳化的乘法器硬體。為了更明了乘法器的原理,在此一一列舉乘法器的3 個版本的改進。我們先假定被乘數和乘數都是正數。
第一代乘法器
初始的設計模擬我們剛才提到的乘法流程,硬體結構如圖 1.14 所示。假定乘數在32 位乘數暫存器里,64 位的積暫存器初始化為0,顯然每一步需要把被乘數左移一位。左移32次之後,被乘數的32 位會被移到左邊,因此我們需要64 位的被乘數暫存器,初始狀態為低32 位是被乘數,高32 位是0。這個暫存器每一步左移一位,和中間結果對齊,進行相加,相加的結果存在被積暫存器里。同時,乘數暫存器右移以決定是×1 還是×0。
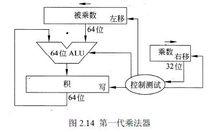 定點乘法器
定點乘法器圖 2.15 說明了進行每1 位乘的3 個基本的操作步驟。第1 步乘數的最低位決定被乘數是否被加到積暫存器中,第2 步的左移操作相當於中間結果左移,第3 步的右移操作給出乘數的下一位以決定相應的操作。上述3 個步驟重複32 次就可以得到乘積的最後結果。
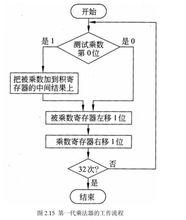 定點乘法器
定點乘法器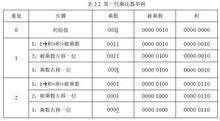 定點乘法器
定點乘法器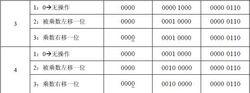 定點乘法器
定點乘法器第二代乘法器
經過仔細觀察我們可以發現,被乘數暫存器的大部分時間有一半位數是 0,W,也就是說只有一半的位數是有用的。在第一代乘法器中,被乘數左移後的位置添0,因此移位後的乘數和中間結果積相加,不影響結果,那么我們可以保持被乘數不動,將中間結果積右移,因此,被乘數暫存器只要32 位即可。圖2.15 和圖2.16 說明了以上改進,圖2.16 是第二代乘法器的硬體結構,圖2.17 是在硬體結構基礎之上的工作流程。
 定點乘法器
定點乘法器 定點乘法器
定點乘法器 定點乘法器
定點乘法器第三代乘法器
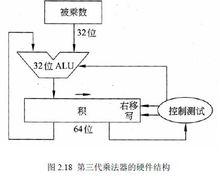
比較善於節省空間的人們發現,積暫存器浪費的空間正好和乘數暫存器浪費的空間一樣,因此,在第三代乘法器中,將積暫存器的右半部分和乘數暫存器結合起來。由圖2.18硬體結構可見,乘數暫存器消失了,初始化時將乘數放在積暫存器的右半部分,左半部分是0。圖2.19 是建立在圖2.18 之上的運算流程。
 定點乘法器
定點乘法器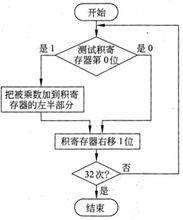 定點乘法器
定點乘法器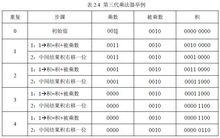 定點乘法器
定點乘法器