解釋
 完全彈性碰撞
完全彈性碰撞碰撞,一般是指兩個或兩個以上物體在運動中相互靠近,或發生接觸時,在相對較短的時間內發生強烈相互作用的過程。
碰撞會使兩個物體或其中的一個物體的運動狀態發生明顯的變化。
碰撞特點
1)碰撞時間極短
2)碰撞力很大,外力可以忽略不計,系統動量守恆
3)速度要發生有限的改變,位移在碰撞前後可以忽略不計
過程分析
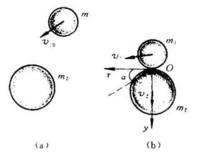
討論兩個球的碰撞過程。碰撞過程可分為 兩個過程。開始碰撞時,兩球相互擠壓,發生形變,由形變產生的彈性恢復力使兩球的速度發生變化,直到兩球的速度變得相等為止。這時形變得到最大。這是碰撞的第一階段,稱為 壓縮階段。此後,由於形變仍然存在,彈性恢復力繼續作用,使兩球速度改變而有相互脫離接觸的趨勢,兩球壓縮逐漸減小,直到兩球脫離接觸時為止。這是碰撞的第二階段,稱為 恢復階段。整個碰撞過程到此結束。
碰撞分類
根據碰撞過程動能是否守恆分為
1) 完全彈性碰撞:碰撞前後系統動能守恆(能完全恢復原狀);
2)非完全彈性碰撞:碰撞前後系統動能不守恆(部分恢復原狀);
3)完全非彈性碰撞:碰撞後系統以相同的速度運動(完全不能恢復原狀)。
一.完全彈性碰撞:能量守恆,動量守恆。
若兩質量為m1,m2的物體,以初速度為v10,v20發生碰撞,設碰撞後的速度各為v1,v2。
則根據:m1v10+m2v20 = m1v1+m2v2
1/2 m1v10^2 + 1/2 m2v20^2 = 1/2 m1v1^2+ 1/2m2v2^2
易證得:v1 = [(m1-m2)v10 + 2m2v20] / (m1+m2)
v2 = [(m2-m1)v20 + 2m1v10] / (m1+m2)
二非彈性碰撞:必須滿足三個約束:1)動量約束:即碰撞前後動量守恆
2)能量約束:即碰撞前後系統能量不增加
3)運動約束:即碰撞前若A物體向右碰撞B物體,那么碰撞後A物體向右
的速度不可超越B物體。
例題
完全彈性碰撞妙趣橫生、耐人尋味,是很特殊的一類碰撞。現擬從七個方面入手,通過一些經典的實例和身邊的現象,仔細“品味”完全彈性碰撞,以期激發學生學習物理的興趣。
如果主碰球的質量為,被碰球的質量為,根據動量守恆和機械能守恆:
解得。
兩和相等
【這個結論再沒有其它任何條件,適用範圍最廣。】
偷梁換柱
 完全彈性碰撞
完全彈性碰撞(1)結論推導:若,則,。(交換速度)(2)典型示例:如圖1所示,在光滑的水平面上有一輛長為的小車A,在A上有一木塊B(大小不計),A與B的質量相等,B與A的動摩擦因數為。開始時A是靜止的,B位於A的正中以初速度向右運動,假設B與A的前後兩壁碰撞是完全彈性的,求B與A的前後兩個牆壁最多能相碰多少次?
解析:先是B在摩擦力的作用下減速,A在摩擦力的作用下加速。地面是光滑的,系統動量守恆,B與A的前壁發生完全彈性碰撞,且質量相等,因此A與B交換速度。此後,B將加速,A將減速,B又與A的後壁發生完全彈性碰撞交換速度。就這樣不停地減速,間斷地交換,最終達到相等的速度,相對運動宣告結束。
,解得。
再根據系統的動能定理,,解得。
在滑動摩擦力中,是相對路程,所以最多能相碰次。
(3)現象連結:如圖2所示,質量相等的兩個剛性小球,擺角不相等,同時由靜止自由釋放,各自將會在自己的半面振動,但是角度不停地周期性變化,對於左面的小球角度的變化是:,右面的小球角度的變化是:。妙趣橫生。
前赴後繼
(1)結論推導:若,且,則,。(傳遞速度)
(2)一題多變:在圖1中,如果B與A之間光滑,B與地面之間的動摩擦因數為,其它條件不變,求B與A的前後兩個牆壁最多能相碰多少次?
解析:先是B在A上無摩擦的滑動,與A的前壁發生短暫的完全彈性碰撞,可以看作動量守恆,由於A與B質量相等,所以它們傳遞速度,B便停下來,A在此速度的基礎上開始減速,接著B與A的後壁又發生完全彈性碰撞傳遞速度,B又勻速運動,A又停止。就這樣二者交換,走走停停,最終系統都停下來。
根據系統的動能定理:,解得。
則B與A的前後兩個牆壁最多能相碰次。
點評:雖然情景相似,但略作變化,結果就大相逕庭。
(3)現象連結:
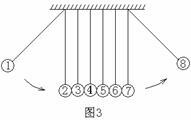
①(英國皇家學會的一個很著名的實驗)它是在天花板上懸掛好多相等擺長的雙線擺,當第一個小球擺下以後,這個速度一直就會傳遞到最後一個小球,最後一個小球也就擺到原來的高度,這樣一直往復運動下去,中間的雙線擺不運動,起到傳遞速度的作用。如圖3所示。
②(檯球)這在檯球運動中是經常見到的現象。
(4)經典回顧:(93年全國高考題)如圖4所示,A、B是位於水平桌面上的兩個質量相等的小木塊,離牆壁的距離分別為和,與桌面之間的動摩擦因數分別為和,今給A以某一初速度,使之從桌面的右端向左運動,假定A、B之間,B與牆壁之間的碰撞時間極短,且碰撞中總動能無損失,若要使木塊A最後不從桌面上掉下來,則A的初速度最大不能超過多少?
解析:物理情景是這樣的,三次碰撞均為完全彈性碰撞:A碰B(前赴後繼),B碰牆(蚍蜉撼樹),B碰A。三段減速運動:A至B,B往返至A,A減速恰至桌面邊緣。
根據質點組的動能定理,
,
解得,。
點評:本題也可以分段列式解答。
勇往直前
(1)結論推導:若,且,則,,。
(2)典型示例:(驗證動量守恆定律的實驗)為了避免入射小球被反向彈回,入射小球的質量必須大於被碰小球的質量,原因就在於此。如圖5所示。
(3)現象連結:一個大人跑步時一不小心碰到一個小孩的身上,小孩很容易被碰倒,就是這個道理。
(4)習題精練:如圖6所示,在光滑水平面上靜止著質量為的物體B,B的一端固連著一根輕質彈簧,質量為的物體A,以的速度沖向B並與之發生正碰,求當彈簧重新回復原長時兩物體的速度各為幾何?
解析:彈簧被壓縮到回復原長的過程,是彈性勢能儲存並完全釋放的過程,動能守恆,發生了完全彈性碰撞,,“勇往直前”,把數據代入篇首的結論,解得:
點評:這個答案可以用第一點“兩和相等”的結論驗證,。
我行我素
(1)結論推導:若,且,則,。
(2)典型示例:(粒子散射實驗)在這個實驗中,首先得排除粒子大角度散射不是電子造成的,課本上為了說明這一點,用了這樣一個比喻:粒子遇到電子就像高速飛行著的子彈遇到一粒塵埃一樣。這個現象可以用以上結論很好的解釋了。
(3)現象連結:鉛球碰撞桌球就是這種現象。
(4)習題精練:見第七點“蚍蜉撼樹”。
反向彈回
(1)結論推導:若,且,則,。
(2)典型示例: 有光滑圓弧軌道的小車質量為,靜止在光滑水平地面上,圓弧下端水平,有一質量為的小球以水平初速度滾上小車,如圖7所示。求小球又滾下和小車分離時二者的速度?
解析:由於滿足動量守恆和動能守恆,所以小球在光滑圓弧上的運動,可以看作是完全彈性碰撞,所以小球的分離可以看作是反向彈回。把數據代入篇首的結論,則
小球的速度:,
小車的速度:。
(3)現象連結:(籃球運動)在籃下,質量小的運動員經常被碰回,這是司空見慣的。
(4)習題精練:如圖8所示,半徑為的光滑圓形軌道固定在豎直面內。小球A、B質量分別為、(為待定係數),A球從左邊與圓心等高處由靜止開始沿軌道開始下滑,與靜止於軌道最低點的B球相碰,碰撞後A、B能達到的最大高度均為,碰撞中無機械能損失,重力加速度為。試求:(1)待定係數;(2)第一次碰撞剛剛結束時小球A、B各自的速度。
解析:(1)由於圓環內側光滑,又碰撞是完全彈性碰撞,所以系統機械能守恆,
,得。
(2)小球A滾下,在最低點的動能是:,解得;
接著與B球發生完全彈性碰撞,被反向彈回,把數據代入篇首的結論,則第一次碰撞剛剛結束時小球A的速度為:,
小球B的速度為:。
點評:
①本題也可以倒過來計算,碰撞之後A、B分別向兩側滑上圓環,機械能守恆
A.; B.。
②在反向彈回的情況下,如果,碰撞之後二者速率相等。
蚍蜉撼樹
(1)結論推導:若,且,則,。
(2)典型示例:(桌球碰撞牆壁)桌球碰倒牆壁以後被反向彈回,它的動量發生了二倍的改變,即。如圖9所示。
(3)現象連結:(氣體分子碰撞器壁)氣體分子頻繁地碰撞器壁,給器壁產生一個持續的恆定的壓力。而每個分子都被反向彈回。
(4)習題精練:網球拍以速率擊中以速率飛來的網球,被擊回的網球的最大速率是多少?(以上所有的速率都是指相對於地面的速率)
解析:最大速率是發生在一條直線上的完全彈性碰撞,設球拍質量為,網球質量為,滿足。
解法一:若球拍靜止,根據以上第七點“蚍蜉撼樹”的結論,網球被反向彈回,速率不變。若網球靜止,根據以上第五點“我行我素”的結論,網球將以的速率飛出。
綜合以上兩點,被擊回的網球的最大速率為:。
解法二:若以球拍為參照系,則網球相對於球拍的速率為,碰撞後以相對速率反向彈回。
再以地面為參照系,球拍相對於地面的速率為,與網球相對於球拍離去速度同向,所以網球對地的速度是:。
解法三:球拍擊球前後速度幾乎不變,即保持不變,根據第一點“兩和相等”得,,因此。
總之,從方方面面“品味”完全彈性碰撞,對掌握其它類型的碰撞是大有裨益的。