由來
一,孿生素數的公式是怎樣得來的
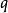 孿生素數公式
孿生素數公式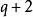 孿生素數公式
孿生素數公式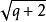 孿生素數公式
孿生素數公式利用素數的判定法則,可以得到以下的結論:「若自然數 與 都不能被任何不大於 的素數 整除,
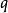 孿生素數公式
孿生素數公式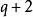 孿生素數公式
孿生素數公式則 與 都是素數,稱為孿生素數」。
 孿生素數公式
孿生素數公式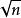 孿生素數公式
孿生素數公式這是因為一個自然數 是素數若且唯若它不能被任何小於等於 的素數整除,就是:
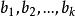 孿生素數公式
孿生素數公式存在一組自然數 ,使得
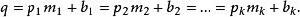 孿生素數公式
孿生素數公式............(1)
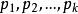 孿生素數公式
孿生素數公式其中 表示從小到大排列時的前k個素數:2,3,5,....。並且滿足
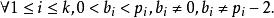 孿生素數公式
孿生素數公式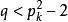 孿生素數公式
孿生素數公式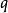 孿生素數公式
孿生素數公式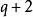 孿生素數公式
孿生素數公式這樣解得的自然數如果滿足 ,則 與 是一對孿生素數。
我們可以把(1)式的內容等價轉換成為同餘方程組表示:
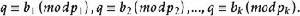 孿生素數公式
孿生素數公式........(2)
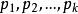 孿生素數公式
孿生素數公式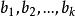 孿生素數公式
孿生素數公式由於(2)的模 都是素數,因此兩兩互素,根據孫子定理,對於給定 ,
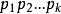 孿生素數公式
孿生素數公式(2)式在 範圍內有唯一一個小於的正整數解。
二,範例
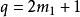 孿生素數公式
孿生素數公式例如k=1時, ,
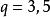 孿生素數公式
孿生素數公式解得 。
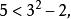 孿生素數公式
孿生素數公式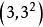 孿生素數公式
孿生素數公式由於,所以可知3與3+2 ;5與5+2都是孿生素數。這樣就求得了區間裡的全部孿生素數對。
又比如k=2時,
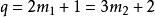 孿生素數公式
孿生素數公式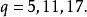 孿生素數公式
孿生素數公式列出方程 ,解得 。
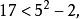 孿生素數公式
孿生素數公式由於 ,所以11與11+2 ;17與17+2都是孿生素數。
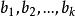 孿生素數公式
孿生素數公式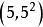 孿生素數公式
孿生素數公式由於這已經是所有可能的 ,值,所以這樣就求得了 區間的全部孿生素數對。
| k=3時 |  孿生素數公式 孿生素數公式 | 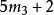 孿生素數公式 孿生素數公式 |  孿生素數公式 孿生素數公式 |
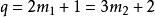 孿生素數公式 孿生素數公式 | 11,41 | 17 | 29 |
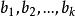 孿生素數公式
孿生素數公式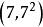 孿生素數公式
孿生素數公式由於這已經是所有可能的值 ,所以這樣就求得了 區間的全部孿生素數對。
 作者王曉明在德國
作者王曉明在德國仿此下去可以一個不漏地求得任意大的數以內的全部孿生素數對。
三,結論推廣
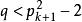 孿生素數公式
孿生素數公式孿生素數猜想就是在k值任意大時,(1)式(2)式都有 d的解。
解。

