簡介
子層是由子群關係對對應的層。
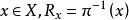 子層
子層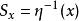 子層
子層設 (R,π,X) 與 (S,η,X) 是 X 上的群層,若 R 是 S 的開子集,η|R=π,且對所有的 是 的子群,則稱 (R,π,X) 是 (S,η,X) 的子層。
子群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
如果群 G 的非空子集合 H 對於 G 的運算也成一個群,那么 H 稱為 G 的子群。 設 G 是群, H 是 G 的非空子集,且 H 關於 G 上的運算也構成群 ,則稱 H 是 G 的子群。
層
數學上,在給定拓撲空間 X上的一個 層(sheaf)(或譯 束、 捆) F對於 X的每個開集給出一個集合或者一個更豐富的結構 F( U) 。這個結構 F( U) 和把開集限制(restricting)到更小的子集的操作相容,並且可以把小的開集粘起來得到更大的。一個 預層(presheaf)和一個層相似,但它可能不可以粘起來。事實上,層使得我們可以用一種細緻的方式討論什麼是 局部性質,就像套用在 函式上的層。
層用於拓撲,代數幾何和微分幾何,只要想跟蹤給定的幾何空間的隨著每個開集變化的代數數據,就可以用層。他們是研究 局部有變化(依賴於所選開集的)的對象的 全局工具。這樣,它們是研究有局部本質的實體的全局行為的自然工具,例如開集,解析函式,流形,等等。
作為一個典型的例子,考慮拓撲空間 X,對於每個 X中的開集 U,令 F( U) 為所有連續函式 U→ R的集合。如果 V是 U的開子集,則 U上的函式可以限制到 V上,而我們得倒映射 F( U) → F( V) 。"粘合"描述了下列過程:假設 U 是給定的開集其並為 U,對於每個 i我們給定一個元素 f∈ F( U) ,一個連續函式 f: U→ R。如果這些函式在重合的地方相等,則我們可以一種唯一的方式把他們粘起來得倒一個連續函式 f: U→ R,它和所有給定的函式 f 一致。所有集合 F( U) 的類和限制映射 F( U) → F( V) 成為一個 X上的集合的層。進一步的,每個 F( U) 是一個交換環,而限制映射是環同態,這使 F成為 X上的環的層。
作為很相似的例子,考慮一個微分流形 X,對於 X的每個開集 U,令 F( U) 為所有可微函式 U→ R的集合。這裡同樣的有粘合,並且我們得倒 X上的環的層。另一個 X上的層是,對於 X的每個開集 U給定所有定義在 U上的可微向量場的向量空間。限制和粘合向量場和函式上的操作一樣,然後我們得倒流形 X上的向量空間的層。

