套代數

套代數是一類重要的非自伴運算元代數，是韌格羅斯(Ringrose,J.R. )於1965年引入的。

簡介

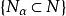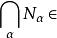套代數是一類重要的非自伴運算元代數。

套代數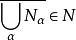

套代數

套代數

設 是希爾伯特空間 H 中的一個閉子空間鏈（即包含關係成為全序的閉子空間族）如果0和H∈，且 關於空間的相交及閉線性張運算封閉（即 蘊涵 ， ，則稱是 H 的一個子空間套，令={T∈(H)|TN⊂N對所有N∈}，則是(H)的弱閉子代數，稱為套代數，或確切地，由子空間套確定的套代數。

發展

套代數是自反運算元代數且其不變子空間格Lat(=)是全序的。

套代數是韌格羅斯(Ringrose,J.R. )於1965年引入的，現在已發展成為系統的理論分支。

自反運算元代數

自反運算元代數是一類重要的非自伴運算元代數。

設是希爾伯特空間H的一族閉子空間，令Alg={T∈(H)|⊂Lat T}，則Alg是包含恆等運算元I的弱閉運算元代數。設⊂AlgLat成立。如果等式成立，即如果=AlgLat，則稱為自反運算元代數。