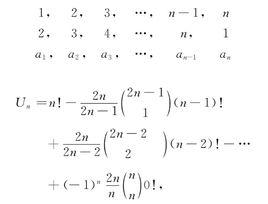基本介紹
Lucas(魯卡斯,法國數學家,1842-1891)曾提出如下的“夫妻問題”:今需安排n對夫妻圍圓桌(2n個座位已編號)而坐,男女相間,夫妻不相鄰,問有多少種不同的安排座位方法?
 夫妻對入座問題
夫妻對入座問題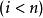 夫妻對入座問題
夫妻對入座問題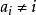 夫妻對入座問題
夫妻對入座問題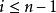 夫妻對入座問題
夫妻對入座問題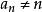 夫妻對入座問題
夫妻對入座問題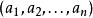 夫妻對入座問題
夫妻對入座問題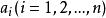 夫妻對入座問題
夫妻對入座問題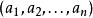 夫妻對入座問題
夫妻對入座問題不妨讓婦女先入坐,共有2n!種方式,然後丈夫再入坐。設婦女已入坐並按環形順序給以1,2,…,n的編號,把第i號婦女的丈夫編號為第i號,把第i號婦女和第i+1號婦女間的位置稱為第i號位置 ,第n號和第1號婦女間的位置稱為第n號位置.現假定男子也已入坐,坐在第i號位置的丈夫的編號為a,按要求 和i+1(當 時), 和1,即要求排列 使得上表中 與同列中前兩行之數無一相重,記這樣的排列 的總數為U,U稱為夫妻數,
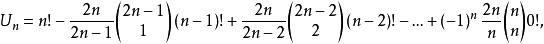 夫妻對入座問題
夫妻對入座問題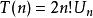 夫妻對入座問題
夫妻對入座問題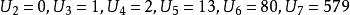 夫妻對入座問題
夫妻對入座問題n≥2,從而 ,易知, 。
相關定理及證明
套用容斥原理容易解決這個似乎很困難的問題 。
定理 n對夫妻圍圓桌(2n個座位已編號)而坐,男女相間,夫妻不相鄰,則不同的坐法數為
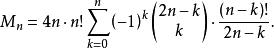 夫妻對入座問題
夫妻對入座問題M稱為夫妻數。
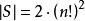 夫妻對入座問題
夫妻對入座問題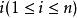 夫妻對入座問題
夫妻對入座問題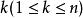 夫妻對入座問題
夫妻對入座問題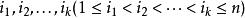 夫妻對入座問題
夫妻對入座問題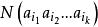 夫妻對入座問題
夫妻對入座問題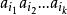 夫妻對入座問題
夫妻對入座問題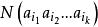 夫妻對入座問題
夫妻對入座問題證明:以S表示n對夫妻男女相間地圍圓桌而坐的全部不同坐法所成之集,則 ,設s∈S,若在坐法s中,第 對夫妻相鄰而坐,則稱s具有性質a,對任意 個正整數 ,以 表示S中同時具有性質 的元素個數,下面求 。
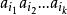 夫妻對入座問題
夫妻對入座問題先設k<n,可依如下4個步驟去作出具有性質 的坐法 。
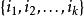 夫妻對入座問題
夫妻對入座問題步驟1:設不在集合 中的最小正整數為j,安排第j對夫妻的丈夫A入座(這樣男女座位編號的奇偶性就確定了),有2n種方法。
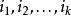 夫妻對入座問題
夫妻對入座問題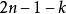 夫妻對入座問題
夫妻對入座問題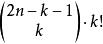 夫妻對入座問題
夫妻對入座問題步驟2:安排第 對夫妻入座,使得每對夫妻相鄰而坐,因為男女座位編號的奇偶性已確定了,所以每對夫妻可看成一個人,他們坐的兩個座位可看成一個座位,故完成步驟2的方法數等於從 個座位中選取k個座位,再把k個人安排在這k個座位上的方法數,為 。
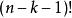 夫妻對入座問題
夫妻對入座問題步驟3:安排餘下的n-k-1個男人入座,有種方法。
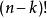 夫妻對入座問題
夫妻對入座問題步驟4:安排餘下的n-k個女人入座,有種方法。
由乘法原則,
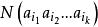 夫妻對入座問題
夫妻對入座問題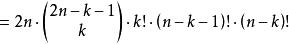 夫妻對入座問題
夫妻對入座問題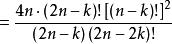 夫妻對入座問題
夫妻對入座問題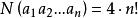 夫妻對入座問題
夫妻對入座問題 夫妻對入座問題
夫妻對入座問題因為 ,故當k=n時上式仍成立,於是由容斥原理,S中不具有 中任一個性質的元素個數,即所求的夫妻數為
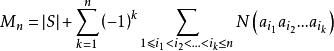 夫妻對入座問題
夫妻對入座問題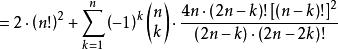 夫妻對入座問題
夫妻對入座問題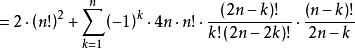 夫妻對入座問題
夫妻對入座問題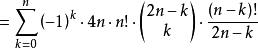 夫妻對入座問題
夫妻對入座問題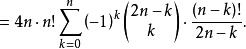 夫妻對入座問題
夫妻對入座問題