多維隨機樣本均值向量

簡介

多維隨機樣本均值向量亦稱樣本均值，多元分析的基本概念之一，是對多維隨機樣本取平均值所得的向量。

具體作法是對每個分量的抽樣取平均值。這裡的樣本是

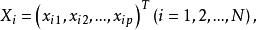多維隨機樣本均值向量

每個分量的平均值是

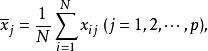多維隨機樣本均值向量

則稱為 p 維隨機樣本的平均值向量，即 p 維隨機樣本均值向量。

多元分析

統計學的一個重要分支，主要探究多維數據的內在規律性，如多維隨機變數間的相互依賴關係、結構關係等。根據獲得數據的類型不同，多元統計分析可分為連續型和離散型多元分析，前者包括多元常態分配的估計與檢驗、多因變數線性回歸、判別分析、典型相關分析、主成分分析、因子分析、聚類分析等，後者包括列聯表分析、對數線性模型、對數單位模型、邏輯斯諦回歸模型、有序離散型多元變數的分析。包括3類：

①多元方差分析、多元回歸分析和協方差分析，稱為線性模型方法，用以研究確定的自變數與因變數之間的關係；

②判別函式分析和聚類分析,用以研究對事物的分類；

③主成分分析、典型相關和因素分析，研究如何用較少的綜合因素代替為數較多的原始變數。