簡介
G的一個自同構如不是內自同構,便稱為外自同構。外自同構群Out(G)的元素是G的內自同構子群Inn(G)在自同構群Aut(G)中的陪集,故其元素不是外自同構,而是可對應到某外自同構加上任何內自同構,因此不能定義G的外自同構群於G上的作用。不過因為內自同構都將群G的元素映射到同共軛類的元素,所以可定義出外自同構群在G的共軛類上的作用。
然而,若G為阿貝爾群,則G的內自同構子群是平凡子群,於是Out(G)可以自然地等同於Aut(G),即是Out(G)的每個元素都對應唯一的自同構,因此Out(G)可以作用於G上。(而這時G的共軛類也各僅有一個元素。)
內自同構
內自同構是一類特殊的自同構。若g是群G中一個元,則映射:
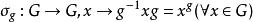 外自同構群
外自同構群給出群G的一個自同構,稱這樣的自同構為群G的內自同構。群G的所有內自同構在映射的合成運算下構成一個群,稱為G的內自同構群,常記為Inn(G)。若G為交換群,則Inn(G)={1}。群G的內自同構群是它的自同構群的正規子群。群G的內自同構群同構於商群G/Z(G),其中Z(G)為G的中心,即Inn(G)G/Z(G)。群G的不是內自構的自同構稱為外自同構。商群Out(G)=Aut(G)/Inn(G)稱為G的外自同構群。外自同構群的元素一般不是自同構。
群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合,a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”,運算結果稱為“乘積”)滿足:
(1)封閉性,a·b∈G;
(2)結合律,即(a·b)c = a·(b·c);
(3)對G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,則稱G對於所定義的運算“·”構成一個群。例如,所有不等於零的實數,關於通常的乘法構成一個群;時針轉動(關於模12加法),構成一個群。
滿足交換律的群,稱為交換群。
群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱,就存在群。例如,可以用研究圖形在變換群下保持不變的性質,來定義各種幾何學,即利用變換群對幾何學進行分類。可以說,不了解群,就不可能理解現代數學。
1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。
同構
兩個數學系統(例如兩個代數系統),當它們的元素及各自所定義的運算一一對應,並且運算結果也保持一一對應,則稱這兩個系統同構,記為≌。它們對於所定義的運算,具有相同的結構。例如,十進制數與二進制數是同構的。
建立同構關係的映射,稱為同構映射。例如,當映射為一一映射,並且對應元素關於運算保持對應時,就是同構映射。
同構是數學中最重要的概念之一。在很多情況,一個難題往往可以化成另一個同構的、似乎與它不相關的、已經解決的問題,從而使原問題方便地得到解決。雖然數學發展得越來越複雜,但利用同構概念,不僅使數學得到簡化,而且使數學變得越來越統一。表面上似乎不同,但本質上等價的結果,可以用統一的形式表達出來。例如,如果四色定理得到了證明,其他數學分支中與它同構的幾十個假設,也同時得到了證明。
自同構群
自同構群是一種特殊的群。指群自身的映射所構成的群。群G的所有自同構在映射的合成運算下構成的一個群,稱為群G的自同構群,常記為Aut(G)。
自同構群是一種重要的幾何變換群。是幾何學分類的依據.設S是給定的空間,U是S上的一個圖形,若S到自身的一個變換g把U變到U自身,則稱g是關於U的自同構變換,簡稱關於U的自同構。S上關於U的自同構變換的全體構成一個變換群,稱它為關於U的自同構群。在變換中保持不變的這個圖形U稱為絕對形。例如,在射影平面上取一條直線作無窮遠直線,則在射影平面上保持無窮遠直線不變的自同構射影變換構成一個變換群,它是關於無窮遠直線的自同構群,同時它也是二維射影變換群的子群,即仿射變換群。
