介紹
在數學內， 墨卡托級數(Mercator series)或者 牛頓-墨卡托級數(Newton–Mercator series)是一個自然對數的泰勒級數：
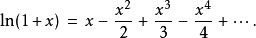墨卡托級數使用大寫sigma表示則為
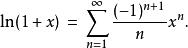墨卡托級數當 −1< x≤1時，此級數收斂於自然對數(加了1)。
歷史
這級數被尼古拉斯·墨卡托，牛頓和Gregory Saint-Vincent分別獨立發現。首先被墨卡托出版於其1668年時的著作 Logarithmo-technica。
推導
這級數可以由泰勒公式導出，藉由不斷地計算第 n次ln x在 x=1時的微分，一開始是
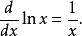墨卡托級數或者，我們可以從有限的等比數列開始( t≠−1)
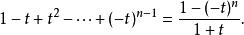墨卡托級數這可以導出
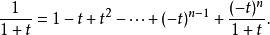墨卡托級數然後得到
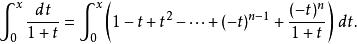墨卡托級數接著逐項積分，
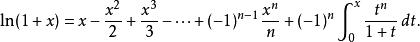墨卡托級數
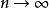墨卡托級數若−1< x≤1，餘項會在時趨近於零。
這個表示法可以重複積分k次，得到
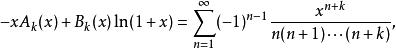墨卡托級數這裡的
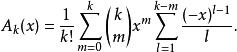墨卡托級數和
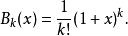墨卡托級數都是 x的多項式。
特例
令墨卡托級數裡面的 x=1，則我們會得到交錯調和級數
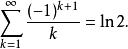墨卡托級數複數級數
下面的複數冪級數
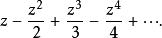墨卡托級數是ln(1+ z)的泰勒級數，這裡ln代表複對數(complex logarithm)的主要分支(principal branch)。這個級數收斂於一個開放的單位圓盤| z|<1 以及圓 | z|=1 ， z=-1除外 (根據阿貝爾判別法)，而且這裡的收斂對每個半徑小於一的圓盤是一致的。
