菲涅耳-基爾霍夫衍射公式
在菲涅耳衍射積分公式提出六十餘年後，古斯塔夫·基爾霍夫用嚴格的數學理論推導出菲涅耳-基爾霍夫衍射公式 ：
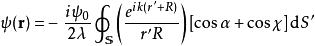基爾霍夫衍射公式
基爾霍夫衍射公式
基爾霍夫衍射公式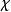
基爾霍夫衍射公式
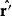基爾霍夫衍射公式
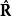基爾霍夫衍射公式其中， 、 分別是 、 與 之間的夾角。
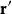基爾霍夫衍射公式
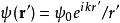基爾霍夫衍射公式 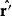基爾霍夫衍射公式 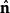基爾霍夫衍射公式
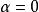基爾霍夫衍射公式
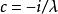基爾霍夫衍射公式
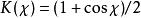基爾霍夫衍射公式推論從點光源Q發射的單色光波，其波擾的數值大小與傳播距離成反比，在位置 以方程表達為 。又在其發射出的球面波的波前任意位置， 與 同向，夾角 。設定比例常數 ， ，則可得到菲涅耳衍射積分公式。
嚴格導引
基爾霍夫衍射公式
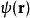基爾霍夫衍射公式 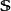基爾霍夫衍射公式點P在閉合曲面 之外。位於點P的波擾 ，可以以位於閉合曲面 的所有波擾與其梯度表達。
基爾霍夫衍射公式基爾霍夫積分定理套用格林第二恆等式來推導出齊次波動方程的解答，這解答是以波動方程在任意閉合曲面 的每一個點的解答和其一階導數來表達。
對於單頻率波，解答為
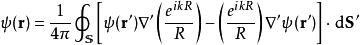基爾霍夫衍射公式或者
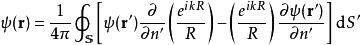基爾霍夫衍射公式
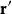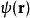基爾霍夫衍射公式 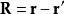基爾霍夫衍射公式 基爾霍夫衍射公式
基爾霍夫衍射公式
基爾霍夫衍射公式
基爾霍夫衍射公式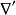
基爾霍夫衍射公式 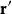基爾霍夫衍射公式
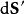基爾霍夫衍射公式 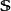基爾霍夫衍射公式
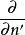基爾霍夫衍射公式 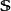基爾霍夫衍射公式其中， 、 分別是從點Q到點P、點Q的位移矢量， 是在點P的波擾， 是從點Q到點P的位移矢量， 是其數值大小， 是波數， 是對於源位置 的梯度， 是從閉合曲面 向外指出的微小面元素矢量， 是閉合曲面 的法嚮導數。
在推導基爾霍夫衍射公式的過程中，基爾霍夫做了以下假定：
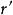基爾霍夫衍射公式
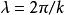基爾霍夫衍射公式點波源與孔隙之間的距離 超大于波長 。
基爾霍夫衍射公式
基爾霍夫衍射公式超大于波長 。
點波源的基爾霍夫衍射
從點波源Q發射的單頻率波，其能量與傳播距離平方成反比，波擾的數值大小與傳播距離成反比，在點Q的波擾以方程表達為
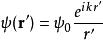基爾霍夫衍射公式
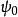基爾霍夫衍射公式其中， 是復值波幅。
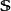基爾霍夫衍射公式假設點P在閉合曲面 之外，套用基爾霍夫積分定理的方程，可以得到在點P的波擾：
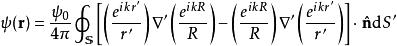基爾霍夫衍射公式 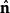基爾霍夫衍射公式 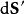基爾霍夫衍射公式其中， 是與 同方向的單位矢量。
注意到球面出射波的梯度為
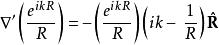基爾霍夫衍射公式
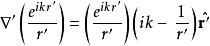基爾霍夫衍射公式
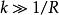基爾霍夫衍射公式
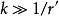基爾霍夫衍射公式從基爾霍夫所做的假定， 、 （例如，假設距離大約為1mm，則對於波長在0.4μm至0.7μm之間的可見光，可以做這假定；但對於波長在1mm至1m之間的微波，這假定不適用），則上述兩個公式近似為
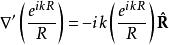基爾霍夫衍射公式
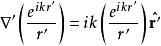基爾霍夫衍射公式所以，在點P的波擾
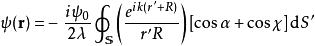基爾霍夫衍射公式 基爾霍夫衍射公式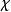 基爾霍夫衍射公式 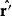基爾霍夫衍射公式 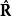基爾霍夫衍射公式 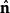基爾霍夫衍射公式其中，、分別是、與之間的夾角。
這就是菲涅耳-基爾霍夫衍射公式，或基爾霍夫衍射公式。
