結構介紹
在模型論,給定在同一個語言L中的兩個結構M和N,我們稱M是N的 基本子結構(有時表示為M<N) 如果
1. M是N的子結構,且
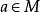 基本子結構
基本子結構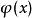 基本子結構
基本子結構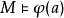 基本子結構
基本子結構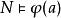 基本子結構
基本子結構2. 對於所有有限元組 ,對於所有語言L的公式 ,我們有 若且唯若 。
我們稱N是M的 基本擴展若且唯若M是N的基本子結構。
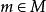 基本子結構
基本子結構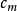 基本子結構
基本子結構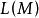 基本子結構
基本子結構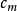 基本子結構
基本子結構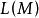 基本子結構
基本子結構有時對第二個條件使用一個等價的陳述。我們可以通過對所有 增加一個常量符號 來擴展L為一個新語言 。那么M和N是解釋每個 為m的 的結構。
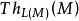 基本子結構
基本子結構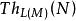 基本子結構
基本子結構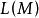 基本子結構
基本子結構設 和 分別是在M和N中為真的 -句子的集合(稱為它們的“基本圖”)。那么上述條件(2)等價陳述
 基本子結構
基本子結構在模型論中,塔斯基-沃特測試是用來判定一個子結構是否是基本子結構的定理。
模型論
模型論(Model theory)是數學的一個學科,模型論的一些重要定理,如緊緻性定理,L-S-T 定理,省略型定理,插值定理等等,不僅對邏輯,集合論,遞歸論的研究有重要作用,而且也在數論、代數、拓撲等數學學科中得到套用。
研究形式語言與其解釋(模型)之間的關係,也就是形式語言的語法與語義之間的關係。數理邏輯的主要分支之一。模型論把形式語言中的公式、句子、理論(句子集)和模型當作數學對象,引進了近世代數中的一些概念、方法,從而模型論的一些結果和方法也被用到數學之中。因此,模型論的一些基本方法,如構造模型的常量方法,圖像方法,模型鏈,超積也已成為常用的方法。一階邏輯的模型論是模型論的基礎,事實上,任何一種邏輯系統都有各自的模型論。 除各種邏輯的模型論外,模型論的新發展層出不窮 ; 用模型論手法來研究邏輯系統,也叫做模型論邏輯;用模型論方法比較各種邏輯系統的強弱,分析各種邏輯系統的特點,叫抽象邏輯的模型論。用遞歸論方法研究模型論問題產生遞歸模型論。只研究有限模型的構造和判定叫有限模型論。 用模型論的思想去研究代數結構、群、環、模、域等叫做代數模型論。研究模型分類的理論叫穩定性理論。現代模型論對計算機科學也有一定影響。
初等等價結構
在數學中,特別是模型論中,給定語言的兩個結構被稱為初等等價的,如果它們的理論相同,就是說任何被一個模型滿足的句子也被另一個模型滿足。若且唯若兩個模型是基本等效的時,一階理論是完整的。例如考慮帶有二元關係符號 '<' 的語言。實數模型 R 和有理數模型 Q 是初等等價的,因為它們都轉換 '<' 為無界稠密線性次序。還存在數論的非標準模型,它包含不只是數 0, 1, 2, 的其他對象。但是這個語言同於標準數論,因為這些額外的對象不能被提及。所以數論的標準模型和非標準模型是初等等價的。
形式語言
數學、邏輯和計算機科學中, 形式語言(英語:Formal language)是用精確的數學或機器可處理的公式定義的語言。
如語言學中語言一樣,形式語言一般有兩個方面: 語法和語義。專門研究語言的語法的數學和計算機科學分支叫做 形式語言理論,它只研究語言的語法而不致力於它的語義。在形式語言理論中, 形式語言是一個字母表上的某些有限長字元串的集合。一個形式語言可以包含無限多個字元串。按一定規律構成的句子或符號串的有限或無限的集合。
形式語言的字母是從該語言的字元串可以形成的一組符號,字母,或標記,;通常它的要求是有限的。
字元串
字元串由這個稱為字的字母形成,這些詞屬於一個特定的形式語言有時被稱為形式公式。一個正式的語言,往往是通過一個正式的語法,如正則文法或上下文無關文法定義,稱作形成規律。形式語言理論主要研究的是內部結構模式這類語言的純粹的語法領域。形式語言理論是從語言學衍生而來,作為一種理解自然語言的句法規律。在計算機科學中,形式語言通常作為定義程式語言和語法的基礎,是正式版本的自然語言的子集。在計算複雜性理論中,決策問題通常定義為形式語言,複雜類被定義為形式語言的集合,它能被具有有限計算能力的機器所解析。在邏輯和數學基礎中,形式語言是用來表示公理系統的語法。
套用
基本子結構在基本結構如集合,序列,求和等中有著廣泛套用。在計算機編譯原理中和自然語言處理也廣泛存在。

