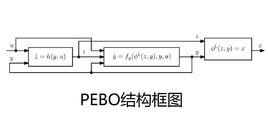
問題描述
對於給定動力系統
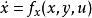基於參數估計觀測器 
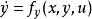基於參數估計觀測器 x,y為系統狀態，u為系統輸入，其中y為可測部分，而x是需要估計狀態，假設系統中所有映射足夠光滑。對於該問題，狀態觀測器設計的目標是設計一個動力系統
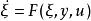基於參數估計觀測器 
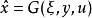基於參數估計觀測器 
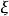基於參數估計觀測器 
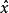基於參數估計觀測器 以保證有界，同時漸近收斂到狀態x。
PEBO的條件
在對動力系統設計觀測器時，系統需要同時滿足三個性質，即可轉化性、左逆性與可辨識性。
可轉化性
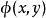基於參數估計觀測器 可轉化性本質上是為一個偏微分方程可解性，即存在一個光滑映射h(y,u)使得如下的PDE需要存在解
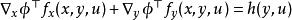基於參數估計觀測器 該偏微分方程在求解中，h(y,u)在自由項（free term），這就提高了PDE可解性，目前已經發現很多物理系統的動力學模型滿足PEBO PDE。這樣可以設計動態擴展（dynamic extension）
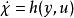基於參數估計觀測器 
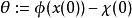基於參數估計觀測器 得到一個參數估計問題，要被估計的參數。
左逆性
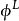基於參數估計觀測器 以上PDE解關於第一項要滿足左可逆條件，即存在映射滿足
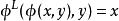基於參數估計觀測器 該條件條件很很多觀測器中均存在，例如I&I觀測器，KKL觀測器等，該假設可以弱化為一定的單射條件。
可辨識性
以上兩個假設將狀態重構轉化為線上參數估計，餘下的核心問題就是該參數（或向量）是否可以被估計出，這就要求系統滿足一致可辨識性，即存在如下參數估計器
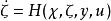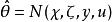基於參數估計觀測器 
基於參數估計觀測器 
基於參數估計觀測器 使得有界，且
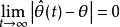基於參數估計觀測器 
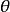基於參數估計觀測器 該假設在具有線性結構的時候，可以類似於持續激勵的條件。
PEBO設計結果
若系統滿足以上三個假設，可以按照上述觀測器定義進行設計PEBO，其中映射選擇如下：
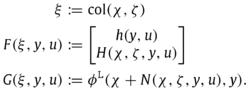基於參數估計觀測器 該PEBO可以所研究的系統的部分狀態x進行漸近估計。
PEBO特點
PEBO在非線性系統觀測器設計中，主要的難點是PDE可解性，還要保證該解的可逆行。類似的觀測器還有I&I觀測器和Kazantzis–Kravaris–Luenberger觀測器，但是它們所要求的PDE不同，因此所能套用的系統也不盡相同。
在PEBO中參數可辨識性要求不高，對於很多非線性參數回歸，可以通過過參數化（over-parameterisation）的方法完成參數估計。
該方法本質上的缺陷是使用了純積分環節，這樣會對輸出端的測量噪聲相對敏感。但PEBO也已經證明在很多其他觀測器無法解決的場合下，可以完成一些複雜的非線性系統的狀態重構任務。
PEBO中的參數估計問題雖然是依賴於軌跡的，但是算法並不脆弱，這是因為參數估計是線上進行的。
系統的能觀性並不意味著系統滿足可轉換性，可轉換性也不意味系統滿足能觀性。
1.PEBO在非線性系統觀測器設計中，主要的難點是PDE可解性，還要保證該解的可逆行。類似的觀測器還有I&I觀測器和Kazantzis–Kravaris–Luenberger觀測器，但是它們所要求的PDE不同，因此所能套用的系統也不盡相同。
2.在PEBO中參數可辨識性要求不高，對於很多非線性參數回歸，可以通過過參數化（over-parameterisation）的方法完成參數估計。
3.該方法本質上的缺陷是使用了純積分環節，這樣會對輸出端的測量噪聲相對敏感。但PEBO也已經證明在很多其他觀測器無法解決的場合下，可以完成一些複雜的非線性系統的狀態重構任務。
4.PEBO中的參數估計問題雖然是依賴於軌跡的，但是算法並不脆弱，這是因為參數估計是線上進行的。
5.系統的能觀性並不意味著系統滿足可轉換性，可轉換性也不意味系統滿足能觀性。
物理系統中的套用
PEBO目前已經證明，在很多其他觀測器無法套用的場景可以提供比較可靠的估計結果，例如無感測器控制下的磁懸浮系統，PMSM電機參數與磁通估計問題 ，化工反應水槽液位估計，PLvCC機械系統，Cuk變壓系統等。
