概念
捷聯慣性導航系統SINS（Strapdown InertiaI Navigation System）在較惡劣的高動態環境下工作時，存在著較大的圓錐誤差，需要對其進行補償，否則，將直接影響精度。這種補償算法即圓錐補償算法。
高速、高精度的圓錐補償算法是提高捷聯慣性導航系統(SINS)性能的重要環節。圓錐誤差的補償主要與陀螺的採樣周期和旋轉矢量修正算法有關。縮短採樣周期可以減小圓錐誤差，但計算量也相應地增大。因此研究合適的旋轉矢量修正算法是克服圓錐誤差的有效途徑。
傳統的圓錐補償算法
圓錐運動是分析圓錐補償算法的典型運動。旋轉矢量微分方程的簡化式：
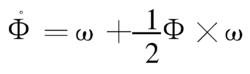圓錐補償算法式中，Φ為旋轉矢量；ω為陀螺輸出的角速率。由上式可以推導出多種求取旋轉矢量的算法， 如單子樣、二子樣、三子樣、四子樣和二子樣疊代算法等都是工程中常用的算法，從算法精度和計算量綜合比較， 三子樣算法比較優越。三子樣算法表達式：
Φ= Δθ1 +Δθ2 +Δθ3 +0 .45(Δθ1 ×Δθ3)+0 .65Δθ2 ×(Δθ3 -Δθ1)
式中，Δθ1，Δθ2，Δθ3 為T ～ T +h 姿態更新周期內陀螺等間隔角增量輸出。而根據這3個角增量只能假定在姿態更新周期內ω為二次多項式：
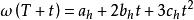圓錐補償算法
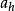圓錐補償算法
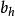圓錐補償算法
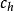圓錐補償算法式中， , , 為姿態更新周期h 內的陀螺角速率多項式係數。此算法的圓錐運動誤差：
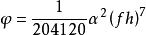圓錐補償算法式中，α為圓錐角；f為圓錐運動的角頻率。
如果陀螺輸出為ω時，需要用數值積分法(如梯形法或辛普生法)由ω提取角增量，再計算Φ。此時該算法的圓錐運動誤差：
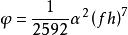圓錐補償算法顯然ω輸入情況下三子樣算法誤差增大，原因是角增量提取過程引入誤差。另外，在姿態更新周期內提取等間隔角增量時也增加了計算量 。
圓錐補償算法的一般形式為：
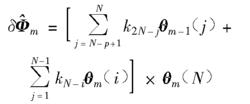圓錐補償算法
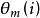圓錐補償算法
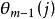圓錐補償算法式中p 為利用的上一周期的數據採樣個數； 為第m 次圓錐補償周期的第i 個角度輸出；為第m- 1次圓錐補償周期中的第j個角度輸出。此表達式仍存在一定程度的誤差, 需進一步修正。
圓錐補償算法最佳化
當以旋轉矢量描述載體姿態運動時，ΔΦ的值為：
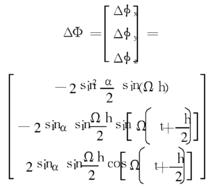圓錐補償算法誤差判據定義為精確的更新旋轉矢量ΔΦ與估計的更新旋轉矢量ΔΦ'之間的差值。而它們的各分量之間只有第1項是非0常值，其餘兩項都呈周期性。因此，定義算法誤差如下:
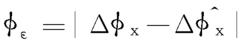圓錐補償算法而該算法誤差會在被修正的四元數中產生漂移誤差，定義為
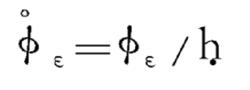圓錐補償算法因此，圓錐補償算法的最佳化準則就是讓Φε的低冪次項為0，以使Φε·最小。
套用
捷聯慣性導航系統SINS（Strapdown InertiaI Navigation System）在較惡劣的高動態環境下工作時，存在著較大的圓錐誤差，需要對其進行補償，否則，將直接影響精度。國內外學者對高精度、高速度的圓錐補償算法進行了大量的研究，取得了許多成就 。通過在典型圓錐運動條件下對算法進行最佳化，得到相應的圓錐補償係數方程和算法誤差表達式。這對於角速率圓錐補償算法快捷有效的套用於工程實踐具有理論意義和實用價值。
