定義
軟體源碼某部分的圈複雜度就是這部分代碼中線性無關路徑的數量 。
舉例
如果一段源碼中不包含控制流語句（條件或決策點），那么這段代碼的圈複雜度為1，因為這段代碼中只會有一條路徑；如果一段代碼中僅包含一個if語句，且if語句僅有一個條件，那么這段代碼的圈複雜度為2；包含兩個嵌套的if語句，或是一個if語句有兩個條件的代碼塊的圈複雜度為3。
計算
它的計算方法很簡單：
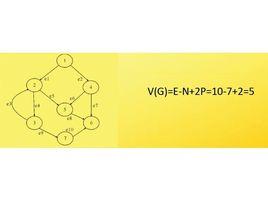
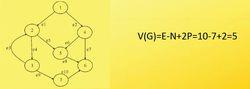
計算公式1：V(G)=e-n+2p。其中，e表示控制流圖中邊的數量，n表示控制流圖中節點的數量，p圖的連線組件數目（圖的組件數是相連節點的最大集合）。因為控制流圖都是連通的，所以p為1.
圈複雜度計算公式2：V(G)=區域數=判定節點數+1。其實，圈複雜度的計算還有更直觀的方法，因為圈複雜度所反映的是“判定條件”的數量，所以圈複雜度實際上就是等於判定節點的數量再加上1，也即控制流圖的區域數。
對於多分支的CASE結構或IF-ELSEIF-ELSE結構，統計判定節點的個數時需要特別注意一點，要求必須統計全部實際的判定節點數，也即每個ELSEIF語句，以及每個CASE語句，都應該算為一個判定節點。
圈複雜度計算公式3：V(G)=R。其中R代表平面被控制流圖劃分成的區域數。
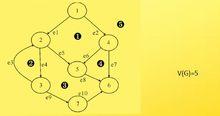圈複雜度針對程式的控制流圖計算圈複雜度V(G)時，最好還是採用第一個公式，也即V(G)=e-n+2；而針對模組的控制流圖時，可以直接統計判定節點數，這樣更為簡單；針對複雜的控制流圖是，使用區域計算公式V(G)=R更為簡單。
