固體中的衝擊波
正文
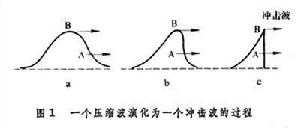
固體中應力、應變和質點速度在波陣面上發生突變的壓縮應力波。一個波剖面如圖1a所示的壓縮應力波在固體中傳播時,在實驗室坐標中,A點狀態以uA+сA的速度向前運動,B點狀態將以uB+сB向前運動(u為粒子速度,с為聲速)。如果uA+cA<uB+cB, (1)
則B點將不斷追趕A點。由於這種追趕的結果,使波陣面變得越來越陡,最終演化為一個具有陡峭陣面特徵的波剖面,形成為圖1c所示的衝擊波。式(1)的等效關係式,即該介質物態方程性質應該滿足的衝擊波穩定性判據是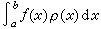 , (2)
, (2)
 固體中的衝擊波
固體中的衝擊波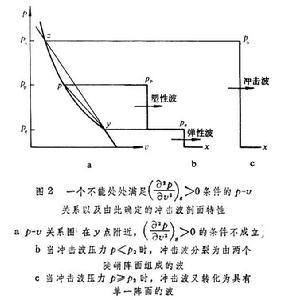 固體中的衝擊波
固體中的衝擊波根據彈塑性理論,一維應變下低壓彈性段的材料性態可以用下式描述
 , (3)
, (3)

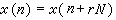 ,下標t、n 分別代表平行於和垂直於波陣面傳播方向上的量。同一體應變下的流體靜壓曲線方程為
,下標t、n 分別代表平行於和垂直於波陣面傳播方向上的量。同一體應變下的流體靜壓曲線方程為
p=Kθ , (4)
式中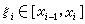 。由於一般介質的 K值隨p 緩慢地增大,故流體靜壓曲線H是下凹的(圖3)。
。由於一般介質的 K值隨p 緩慢地增大,故流體靜壓曲線H是下凹的(圖3)。 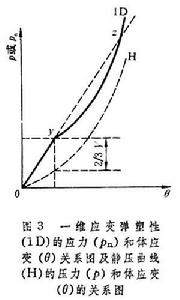 固體中的衝擊波
固體中的衝擊波 (5)
(5)
 , (6)
, (6)
pn=p+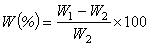 (7)
(7)
從式(7)看出,當進入塑性區後,由於一維應變曲線與流體靜壓曲線在壓力坐標上僅差一個常數因子
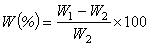 ,因此隨著壓力的增高,用p代替pn所引起的相對誤差會越來越小。一般認為,當衝擊波壓力大於介質的許貢紐彈性極限的6~8倍後,即可用流體靜壓曲線代替一維應變曲線。由於一般固體材料的py約為10千巴,故當衝擊壓力大於10萬巴時,通常可以把實測的一維衝擊壓縮曲線當作流體靜壓曲線處理。這種處理方法為把衝擊壓縮曲線與靜態壓縮曲線(一個等溫過程的流體靜壓曲線)的直接比較提供了方便。
,因此隨著壓力的增高,用p代替pn所引起的相對誤差會越來越小。一般認為,當衝擊波壓力大於介質的許貢紐彈性極限的6~8倍後,即可用流體靜壓曲線代替一維應變曲線。由於一般固體材料的py約為10千巴,故當衝擊壓力大於10萬巴時,通常可以把實測的一維衝擊壓縮曲線當作流體靜壓曲線處理。這種處理方法為把衝擊壓縮曲線與靜態壓縮曲線(一個等溫過程的流體靜壓曲線)的直接比較提供了方便。