正文
。通過對遺傳現象的大量觀察統計，人們發現子女身高與父母身高之間有一定關係。平均來看，若父母很高，他們的子女並不會像父母那樣高，而父母很矮，他們的子女也不像父母那樣矮。這種遺傳身高趨於一般的現象，稱為回歸。後來回歸一詞被用來描述多個隨機變數之間在統計平均意義上趨向於某種較為確定的相互依賴關係，即統計相關關係。通過回歸分析找到多個變數之間的統計相關關係，就能建立回歸方程式。例如，尳＝f(x1,x2),式中y為因變數,尳為對y的估計值;x1和x2為自變數。在對自變數x1和x2控制或預測的基礎上,就能對因變數y作出預測。回歸法在經濟領域中的典型套用是計量經濟模型（見計量經濟學）。特點
用回歸法進行預測首先要對各個自變數作出預測。若各個自變數可以由人工控制或易於預測，而且回歸方程也較為符合實際，則套用回歸法預測是有效的，否則就很難套用。為使回歸方程較能符合實際，首先應儘可能定性判斷自變數的可能種類和個數，並在觀察事物發展規律的基礎上定性判斷回歸方程的可能類型。其次，力求掌握較充分的高質量統計數據，再運用一套統計和檢驗程式，利用數學工具從定量方面計算或改進前兩種定性判斷。分類
回歸法按照所採用主方程分類。回歸方程可以是代數函式、超越函式或它們的混合形式。回歸方程為線性的稱為線性回歸，否則稱為非線性回歸。自變數只有一個的稱為單元回歸，多於一個的稱為多元回歸。① 單元線性回歸 只有一個自變數的線性回歸,用於兩個因素（如y和x）接近線性關係的場合。相應的回歸方程式為
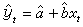，式中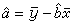
,而墖和?是分別根據y和x的一組已知觀測值（yi，xi）（i=1，…,n）用最小二乘法求出的最小二乘估計值;峹 =lxy／lxx,表示估計值尳t相對於觀察值xt的變化率，稱為回歸係數。
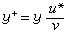,稱為x和y的相關係數，它越接近1,x和y的線性相關程度就越大。
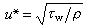，稱為剩餘標準差，它越小，採樣點就越接近回歸方程式。
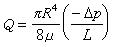，稱為x的自方差； 
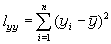，稱為y的自方差;
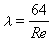,稱為x、y的協方差。在簡單情況下，回歸法就是消耗係數法或生產係數法。例如,峹可以表示生產每噸鋼消耗多少度電，一噸化肥能增產多少噸糧食等。這種係數在投入產出表（見投入產出法）中是經常使用的。 ② 多元線性回歸 用於一個因變數 y同多個自變數x1,x2,…, xm 線性相關的問題。相應的回歸方程式為
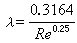。回歸係數峹k(k＝0,1,…,m)可由觀測值按最小二乘法確定。 ③ 非線性回歸 分為兩類：一類可通過數學變換變成線性回歸，如取對數可使乘法變成加法等；另一類可直接進行非線性回歸，如多項式回歸。
④ 單元多項式回歸 因變數同自變數成多項式函式關係的回歸法，相應的回歸方程為
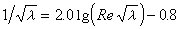,式中姙k(k＝0,1,…,m)可由觀察值按最小二乘法確定。 