簡介
曲線回歸(curve regression) 是建立不同變數間相關關係的非線性數學模型數量關係式的統計方法,也稱為 非線性回歸。農業化學中各種因素間的相互關係多數是曲線關係。
可化為直線的回歸
可化為直線的回歸是曲線回歸中套用最廣泛的形式。對某種形式的曲線回歸模型取一定形式的變數變換,轉換為線性回歸模型,即可將曲線回歸以線性回歸的方法計算出式中各項參數,並進行統計檢驗和推斷。可化為直線的曲線回歸種類多樣,常用的見表。
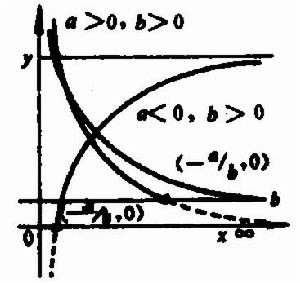 圖1 圖1 | 公式: 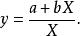 回歸曲線 回歸曲線 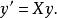 回歸曲線 回歸曲線 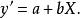 回歸曲線 回歸曲線 |
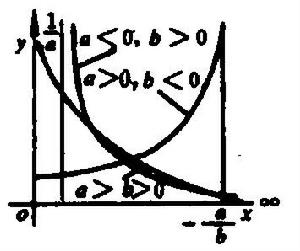 圖2 圖2 | 公式: 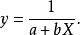 回歸曲線 回歸曲線 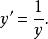 回歸曲線 回歸曲線 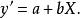 回歸曲線 回歸曲線 |
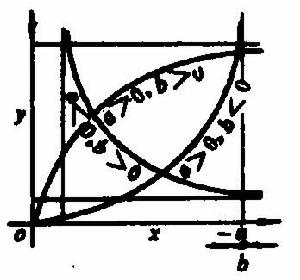 圖 3 圖 3 | 公式: 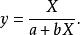 回歸曲線 回歸曲線 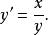 回歸曲線 回歸曲線 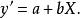 回歸曲線 回歸曲線 |
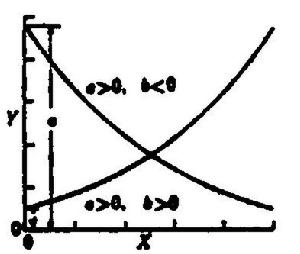 圖4 圖4 | 公式: 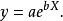 回歸曲線 回歸曲線 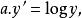 回歸曲線 回歸曲線 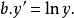 回歸曲線 回歸曲線 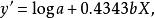 回歸曲線 回歸曲線 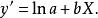 回歸曲線 回歸曲線 |
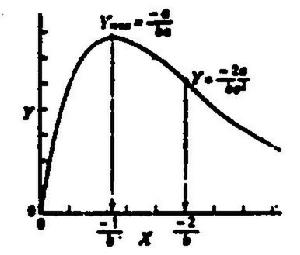 圖5 圖5 | 公式: 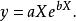 回歸曲線 回歸曲線 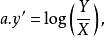 回歸曲線 回歸曲線 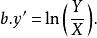 回歸曲線 回歸曲線 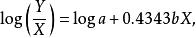 回歸曲線 回歸曲線 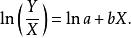 回歸曲線 回歸曲線 |
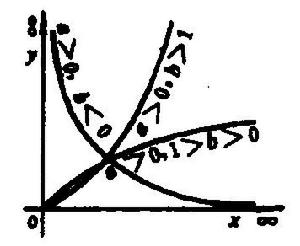 圖5 圖5 | 公式: 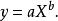 回歸曲線 回歸曲線 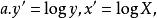 回歸曲線 回歸曲線 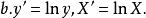 回歸曲線 回歸曲線 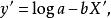 回歸曲線 回歸曲線 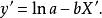 回歸曲線 回歸曲線 |
正交多項式回歸
關於多項式回歸,可參考相應詞條。
多元線性回歸及多項式回歸的計算量隨待估參數的數目增多而大量增加,而且各因素之間存在相關性。若需剔除不顯著因素,則其他因素的回歸係數需重新計算。解決這些困難的最常用辦法是採用正交多項式,其前提是試驗因素的水平間隔h要相等。對等間距水平的試驗引進一族正交多項式,經數據變換後符合正交條件,從而消除了各因素之間相關性,並簡化計算過程。正交多項式同樣適用於多元多項式回歸。
生長曲線
作物及養分吸收在生長初期較慢,達一定時間後積累迅速,以後又逐漸減緩,這種曲線大多呈S形,統稱為 生長曲線。這種理論曲線的模型呈正態曲線或近似於正態曲線。施肥對生長曲線的模型參數有明顯影響,故在農業化學研究中亦常用生長曲線。生長曲線可分為從正態曲線假定出發及不以正態曲線出發兩類。以正態假設出發的典型曲線是對稱的S形曲線,其理論依據是將試驗數據y轉化為正態累積函式的標準差單位μ,當處理的水平變數為X時,則:
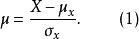 回歸曲線
回歸曲線式(1)中μ、σ分別為變數X的總體平均值與標準差。對特定總體μ、σ為常數。故:
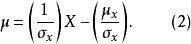 回歸曲線
回歸曲線y值轉換為正態離差後,X與μ呈線性關係。由於正態累積函式的標準差單位有正值和負值,為便於計算,定義ρ=μ+5以消去負值,P稱為機率單位。p與μ只相差常量5,不改變曲線形態,於是式(2)轉化為式(3)
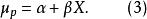 回歸曲線
回歸曲線式(3)中
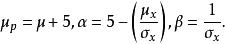 回歸曲線
回歸曲線有時生長曲線呈不對稱分布的S形,常對處理變數X取對數變換,則式(2)、式(3)成式(4)、式(5)形式,而成為正態曲線:
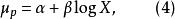 回歸曲線
回歸曲線 回歸曲線
回歸曲線不以正態曲線出發的S形曲線有更廣泛的適用範圍,最著名的是洛傑蒂克(Logistic)生長曲線:
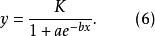 回歸曲線
回歸曲線農化試驗取得試驗數據往往可用不同數學模型擬合,從中選定最適的模型可以縮小模型誤差,這就需要從各種曲線回歸模式中選擇誤差最小的一種,同時要注意儘可能在專業知識方面得到合理的解釋。