簡介
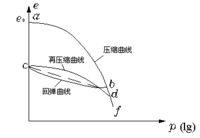 回彈曲線
回彈曲線常規的壓縮曲線是在試驗中連續遞增加壓獲得的,如果加壓到某一值 p i;(相應於圖中曲線上的 b點)後不再加壓,而是逐級進行卸載直至零,並且測得各卸載等級下土樣回彈穩定后土樣高度,進而換算得到相應的孔隙比,即可繪製出卸載階段的關係曲線,如圖中 bc曲線所示,稱為回彈曲線(或膨脹曲線)。可以看到不同於一般的彈性材料的是,回彈曲線不和初始載入的曲線 ab重合,卸載至零時,土樣的孔隙比沒有恢復到初始壓力為零時的孔隙比 e。這就顯示了土殘留了一部分壓縮變形,稱之為 殘餘變形,但也恢復了一部分壓縮變形,稱之為 彈性變形。若接著重新逐級加壓,則可測得土樣在各級荷載作用下再壓縮穩定後的孔隙比,相應地可繪製出再壓縮曲線,如圖4-3中 cdf曲線所示。可以發現其中 df段像是 ab段的延續,猶如其間沒有經過卸載和再壓的過程一樣。卸載段和再壓縮段的平均斜率稱為回彈指數或再壓縮指數 C。通常 C<< C,一般粘性土的 C≈(0.l~0.2) C。
彈塑性增量理論
彈塑性增量理論,又稱增量理論,是由聖維南於1871 年提出的,提出了塑性應變增量主軸和應力變數主軸重合的重要假設,為塑性理論的發展奠定了基礎;同年,列維近一步提出:在塑性變形過程中,塑性應變增量分量與對應的偏應力分量成比例,並建立了 Levy-Mises 塑性增量理論。在此基礎上,1924 年,普朗特考慮到金屬屈服後應包括彈性應變部分,1930 年羅伊斯將這一理論推廣到三維應力問題,完善並建立了普朗特—羅伊斯塑性增量理論。包括下述基本假設:1)材料是不可壓縮的。對金屬材料而言, 即使在高壓狀態下,根據彈性理論可知物體在平均正應力的作用下,所引起的變形只有彈性體積變形,不會引起塑性體積變形;但在應力偏量作用下,會使物體產生畸變,但體積不發生變形。物體的畸變又包括彈性變形和塑性變形兩部分, 也就是說塑性變形僅由應變偏量引起, 同時認為塑性狀態下體積變形等於零。2)應變偏量與應力偏量成比例。由於應力羅德參數代表應力莫爾圓的相對位置, 應變增量羅德參數代表應變增量莫爾圓的相對位置, 因此應力羅德參數與應變增量羅德參數之間的關係可以通過大量實驗確定。3)材料是理想剛塑性的,L- M 理論在推導過程中均考慮了塑性應變增量, 因此是基於剛塑性模型建立的 。
固結試驗
固結試驗,又稱壓縮試驗、壓密試驗。用以測定土在完全側限(指側向不發生變形)條件下承受垂直壓力後的壓縮特性的試驗。可分為常規固結試驗、快速固結試驗、高壓固結試驗和連續加荷固結試驗。試驗儀器稱固結儀,有多種型號。試驗時先用內徑61.8mm、高20mm的環刀在土樣上切取試樣,兩端用鋼絲鋸整平後連同環刀一起裝入試驗容器中,後在完全側限和容許豎向排水的條件下分級加壓,記錄壓力、試樣發生的壓縮變形量及其相應的時間,用以計算土的壓縮模量和壓縮指數等表示土的壓縮特性的參數。如在分級加荷後分級卸荷,即為加荷與卸荷回彈試驗,可用以測定土的回彈指數。

