介紹
哈爾小波轉換是於1909年由Alfréd Haar所提出，是小波變換（Wavelet transform）中最簡單的一種變換，也是最早提出的小波變換。他是多貝西小波的於N=2的特例，可稱之為D2。
哈爾小波的母小波（mother wavelet）可表示為：
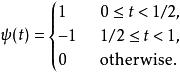哈爾小波轉換且對應的尺度函式（scaling function）可表示為：
哈爾小波轉換其濾波器（filter）h[n]被定義為
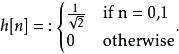哈爾小波轉換當n = 0與n = 1時，有兩個非零係數，因此，我們可以將它寫成
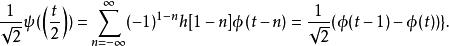哈爾小波轉換在所有正交性（orthonormal）小波變換中哈爾小波轉換（Haar wavelet）是最簡單的一種變換，但它並不適合用於較為平滑的函式，因為它只有一個消失矩（Vanishing Moment）。
哈爾變換
Haar Transform最早是由A. Haar在1910年“Zur theorie der orthogonalen funktionensysteme”中所提出，是一種最簡單又可以反應出時變頻譜（time-variant spectrum）的表示方法。其觀念與Fourier Transform相近，Fourier Transform的原理是利用弦波sine與cosine來對信號進行調變；而Haar Transform則是利用Haar function來對信號進行調變。Haar function也含有sine、cosine所擁有的正交性，也就是說不同的Haar function是互相orthogonal，其內積為零。
以下面的哈爾變換矩陣為例，我們取第一行和第二行來做內積，得到的結果為零；取第二行和第三行來做內積，得到的結果也是零。依序下去，我們可以發現在哈爾變換矩陣任取兩行來進行內積的運算，所得到的內積皆為零。
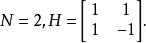哈爾小波轉換
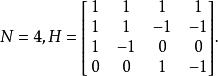哈爾小波轉換
哈爾小波轉換在此前提下，利用Fourier Transform的觀念，假設所要分析的信號可以使用多個頻率與位移不同的Haar function來組合而成，進行Haar Transform時，因為Haar function的正交性，便可求出信號在不同Haar function（不同頻率）的情況下所占有的比例。
套用
說明
由於數字圖片檔案過大，因此我們往往會對圖片做圖像壓縮，壓縮過後的檔案大小不僅存放於電腦中不會占到過大容量，也方便我們於網路上傳送。哈爾小波轉換其中一種套用便是用來壓縮圖像。壓縮圖像的基本概念為將圖像存成到一矩陣，矩陣中的每一元素則代表是每一圖像的某畫素值，介於0到255間。例如256x256大小的圖片會存成256x256大小的矩陣。JPEG影像壓縮的概念為先將圖像切成8x8大小的區塊，每一區塊為一8x8的矩陣。
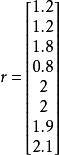哈爾小波轉換在處理8x8二維矩陣前，先試著對一維矩陣作哈爾小波轉換，
哈爾小波轉換公式為。
範例
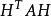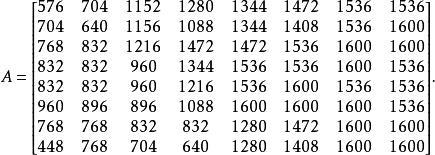
哈爾小波轉換對8x8的二維矩陣A作哈爾小波轉換，由於AH是對A的每一行作哈爾小波轉換，作完後還要對A的每一列作哈爾小波轉換，因此公式為。以下為一簡單的例子：
哈爾小波轉換列哈爾小波轉換（row Haar wavelet transform）
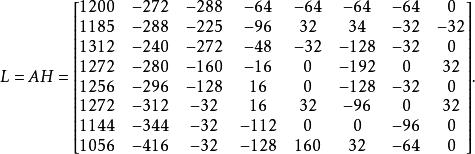哈爾小波轉換行哈爾小波轉換（column Haar wavelet transform）
哈爾小波轉換
哈爾小波轉換 哈爾小波轉換 哈爾小波轉換 哈爾小波轉換由以上例子可以看出哈爾小波轉換的效果，原本矩陣中變化量不大的元素經過變換後會趨近零，再配合適當量化便可以達到壓縮的效果了。此外若一矩陣作完哈爾小波轉換後所含的零元素非常多的話，稱此矩陣叫稀疏，若一矩陣越稀疏壓縮效果越好。因此可對定一臨界值若矩陣中元素的絕對值小於此臨界值，可將該元素令成零，可得到更大的壓縮率。然而取過大的話會造成圖像嚴重失真，因此如何取適當的也是值得討論的議題。
運算量
•若套用於區域的頻譜分析及偵測邊緣的話，離散傅立葉變換、Walsh-Hadamard變換及哈爾小波轉換的計算量見下表
| Running Time | terms required for NRMSE < | |
| 離散傅立葉變換 | 9.5秒 | 43 |
| 沃爾什變換 | 2.2秒 | 65 |
| 哈爾小波轉換 | 0.3秒 | 128 |
