基本介紹
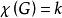 哈德威格猜想
哈德威格猜想哈德威格猜想(Hadwiger 1943,1958):對所有的正整數k,每個滿足的圖一定含有K作為幼圖。
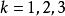 哈德威格猜想
哈德威格猜想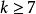 哈德威格猜想
哈德威格猜想當時,哈德威格猜想很容易被驗證。Hadwiger和Dirac證明了當k=4時,猜想成立。Wagner和Robertson,Seymour和Thomas分別證明了當k=5和k=6時,猜想與四色定理等價。對,猜想看起來是圖論中最難解決的問題之一 。
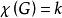 哈德威格猜想
哈德威格猜想Hajós曾經考慮過另一個更強的猜想:每個的圖一定含有一個K的細分。當k≤4時,Hajós這個猜想已被驗證。對每個k≥7, Catlin(1979)找到了Hajós猜想的反例。從而Hajós的這個猜想只在k=5和k=6時仍未解決。
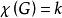 哈德威格猜想
哈德威格猜想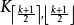 哈德威格猜想
哈德威格猜想受到Kuratowski定理的啟發,Chartrand,Geller和Hedetniemi猜想每個滿足的圖或者含有一個K的細分,或者含有一個的細分。但Hanson和Toff(1994),可能還有Woodall(1990),注意到Catlin的關於Hajós上述猜想的反例也是Chartrand等人的這個猜想的反例。後來Woodall把這個猜想作了修正重新提出如下:
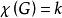 哈德威格猜想
哈德威格猜想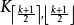 哈德威格猜想
哈德威格猜想猜想(Chartrand,Geller和Hedetniemi 1971,Woodall 1990)對所有正整數k,每個滿足的圖一定含有一個同構於K或的幼圖。
此猜想顯然要弱於哈德威格猜想 。
哈德威格猜想的相關證明
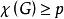 哈德威格猜想
哈德威格猜想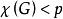 哈德威格猜想
哈德威格猜想1943年,Hadwiger提出了一個關於圖的色數的猜想,除少數幾種情況外,這一猜想至今沒有得到解決。這不足為奇,因為這一猜想的一個實例的真實性等價於平面圖4著色的存在性。這一猜想斷言:色數滿足的連通圖G能收縮到K。等價地,如果G不能收縮到K,那么。該猜想的逆命題為假,即存在可以收縮到K且色數小於p的平面圖。例如,把其邊排成一個圈的4階圖有色數2,然而這個圖本身通過收縮一條邊能收縮到K。
定理1 Hadwiger猜想對於p=5成立若且唯若每個平面圖有4著色 。
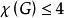 哈德威格猜想
哈德威格猜想部分證明 我們只證明,如果Hadwiger猜想對p=5成立,那么每個平面圖G有4著色。設G是平面圖並且假設G能收縮到K,因為平面圖的收縮還是平面圖,這就推出K是平面圖,從而得到一條假命題,因此G不能收縮到K,所以Hadwiger猜想對於p=5為真推出。
我們已經知道,Hadwiger猜想對於p≤4和p=6為真。下面的定理證明Hadwiger猜想對於p=2,3的情形,至於p=4的情形留作練習。
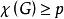 哈德威格猜想
哈德威格猜想定理2 設戶p≤3,如果G是色數滿足的連通圖,那么G能收縮到K。
證明 如果p=1,那么通過每條邊的收縮,我們得到K。如果p=2,那么G至少有一條邊α,除α外收縮所有邊,我們得到K。現在假設p=3,Χ(G)≥3。因為X(G)≥3,所以G不是二分圖,根據定理可知,G有一條長度為奇數的圈。設γ是G中一條長度最小的奇數圈。則只有連線γ中頂點的邊才是γ的邊,否則我們能找一條長度比γ更短的奇數圈,除γ中的邊外,收縮G中所有的邊而得到γ。我們可以進一步收縮邊,直到獲得K。

