哈密頓方程組

哈密頓方程組（Hamilton system）是與歐拉-拉格朗日方程組等價的一階微分方程組。

簡介

哈密頓方程組是與歐拉-拉格朗日方程組等價的一階微分方程組。

以最簡變分積分J(y)為例，做變換

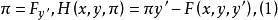哈密頓方程組

則J(y)相應的二階歐拉-拉格朗日方程可化為以y,π為未知函式的一階微分方程組

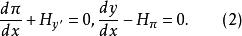哈密頓方程組

正是兩個未知函式的變分積分

哈密頓方程組

的歐拉-拉格朗日方程。

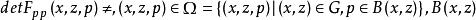哈密頓方程組

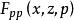哈密頓方程組

一般地，設一元向量函式的變分積分的拉格朗日函式 F(x,z,p) 滿足是 R 中的開集， 是以

哈密頓方程組

為元素的 N×N 矩陣，做勒讓德變換

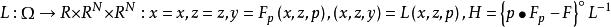哈密頓方程組

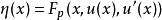哈密頓方程組

令，η 稱為矩，二階歐拉-拉格朗日方程轉換化為一階方程組

哈密頓方程組

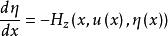哈密頓方程組

這個方程組稱為典範方程組或哈密頓方程組，H 稱為哈密頓函式。

性質

光程函式 S滿足哈密頓-雅可比方程

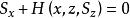哈密頓方程組

哈密頓方程組是變分積分

哈密頓方程組

或

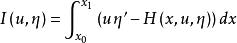哈密頓方程組

的歐拉-拉格朗日方程，若哈密頓函式不顯含 x ，則 H 是運動常量，即沿任何解u(x)，H 是常數。