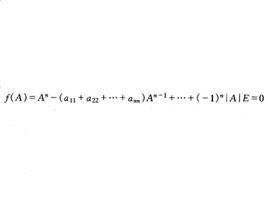哈密頓一凱萊定理

哈密頓-凱萊定理(Hamilton-Cayley theorem)是矩陣的一個重要性質，該定理表述為：設A是數域P上的n階矩陣，f(λ)=|λE-A|=λ+b1λ+…+bn-1λ+bn是A的特徵多項式，則f(A)=A+b1A+...+bn-1A+bnE=0。哈密頓(W.R.Hamilton)在他所著《四元數講義》一書中，涉及線性變換滿足它的特徵多項式的問題，凱萊(A.Cayley)在1858年的一篇文章中，對n=3的情形驗證了此定理，但認為沒有必要進一步證明，弗羅貝尼烏斯(F.G.Frobenius)於1878年給出該定理第一個一般性的證明 。

基本介紹

下面討論方陣A的特徵多項式的一個重要性質——Hamilton-Cayley定理，為證明此定理，先作以下準備：

以F[λ]中的多項式為元素的矩陣稱為λ-矩陣，記為A(λ)，B(λ)，...，例如

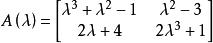哈密頓一凱萊定理

是一個λ-矩陣，按照矩陣加法，數量乘法的定義，A(λ)可以寫成

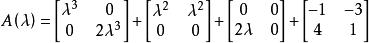哈密頓一凱萊定理

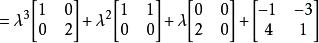哈密頓一凱萊定理

其中λ 的係數都是F上的矩陣，顯然這種表示法是惟一的。一般地，一個m×n的λ-矩陣A(λ)可以惟一表示成多項式：

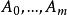哈密頓一凱萊定理

A(λ)=λA+λA+...+λA+A
其中

是數域F上m×n矩陣，(1)式右端稱為矩陣多項式，若A≠0,m稱為矩陣多項式的次數。

定理1(Hamilton-Cayley定理)設A是數域F上的n階矩陣，f(λ)=|λE-A|是A的特徵多項式，則

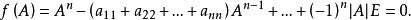哈密頓一凱萊定理

哈密頓-凱萊定理的證明

證明設B(λ)是矩陣λE-A的伴隨矩陣，則：

B(λ)(λE-A)=|λE-A|E=f(λ)E. (2)

因為B(λ)的元素是|λE-A|的元素的代數餘子式，所以B(λ)的元素是次數不超過n-1的λ的多項式，因此B(λ)可寫成：

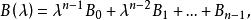哈密頓一凱萊定理

因而

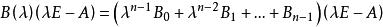哈密頓一凱萊定理

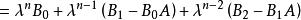哈密頓一凱萊定理

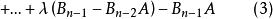哈密頓一凱萊定理

由A的特徵多項式f(λ)是n次的，可設

哈密頓一凱萊定理

則

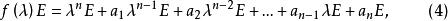哈密頓一凱萊定理

由(2)式，比較(3),(4)兩式得

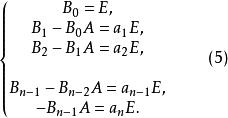哈密頓一凱萊定理

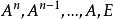哈密頓一凱萊定理

依次用右乘(5)的第1,2,...,n+1式，得

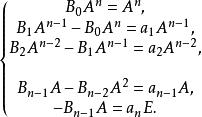哈密頓一凱萊定理

上式兩端分別相加，左邊為0，右邊為f(A)，故f(A)=0，定理得證。

用線性變換的語言敘述Hamilton-Cayley定理：

定理2設σ是n維線性空間V的線性變換，f(λ)是σ的特徵多項式，那么f(σ)=0。
下面利用Hamilton-Cayley定理將線性空間按特徵值分解成不變子空間的直和。

定理3設V是數域F上的n維線性空間，V的線性變換σ的特徵多項式是f(λ)，它可以分解成

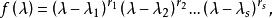哈密頓一凱萊定理

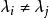哈密頓一凱萊定理

這裡,當時,則V可分解成σ子空同的直和

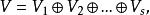哈密頓一凱萊定理

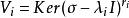哈密頓一凱萊定理

其中。