基本介紹
合取消去規則是邏輯演算規則之一。意思是說，如果一個合取命題是真的，那么它的每個支命題都是真的。
合取消去規則是某些自然推理系統中的推理規則之一。簡記為∧E或者∧。可表述為兩種形式 ：
(1)若Γ├A∧B，則Γ├A;
(2)若Γ├A∧B，則Γ├B。
其中Γ是任意的公式的集合，A、B是公式，├是推出關係。
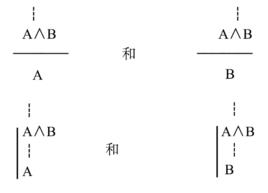
這一規則意為：若Γ可以推出A與B的合取式A∧B，則Γ可以推出A，Γ也可以推出B。這一規則又可用如下的圖式來表示：
合取消去規則也可以表述為如下的圖式 ：
合取消去規則例如：
公民、法人的合法的民事權益受法律保護，
公民的合法的民事權益營法律僳護。
相關概念
謂詞邏輯的自然推理系統
直覺主義謂詞邏輯的自然推理系統是由根岑於1934年建構的推理系統。簡記為系統IQN。它的初始符號中有邏輯聯結詞和量詞¬(否定)、∧(合取)、∨(析取)、→(直覺主義蘊涵)、ᗄ(全稱量詞)、∃(存在量詞)，對它們可以作直覺主義的構造性解釋。系統IQN包含如下的推理規則：肯定前提規則、合取引入規則、析取引入規則、蘊涵引入規則、否定引入規則、合取消去規則、析取消去規則、蘊涵消去規則、否定消去規則、全稱量詞引入規則、存在量詞引入規則、全稱量詞消去規則、存在量詞消去規則。系統IQN是經典謂詞邏輯的自然推理系統QN的真子系統。“間接證明規則”不是系統IQN中有效的推理規則，如果把“間接證明規則”添加到系統IQN中去，就得到了經典謂詞邏輯的自然推理系統QN，即系統QN=系統IQN+間接證明規則。系統IQN等價於公理化的直覺主義謂詞演算IQ，在語義解釋(模型)的基礎上，可以證明系統IQN的可靠性和完全性 。
命題邏輯的自然推理系統
直覺主義命題邏輯的自然推理系統是由根岑於1934年建構的推理系統。簡記為系統IPN。它的初始符號中有邏輯聯結詞¬(否定)、∧(合取)、∨(析取)和→(直覺主義蘊涵)，對它們可以作直覺主義的構造性解釋。系統IPN包含如下的推理規則：肯定前提規則、合取引入規則、析取引入規則、蘊涵引入規則、否定引入規則、合取消去規則、析取消去規則、蘊涵消去規則、否定消去規則。系統IPN是經典命題邏輯的自然推理系統PN的真子系統。“間接證明規則”不是系統IPN中有效的推理規則，如果把“間接證明規則”添加到系統IPN中去，就得到了經典命題邏輯的自然推理系統PN，即系統PN=系統IPN+間接證明規則。系統IPN等價於公理化的直覺主義命題演算IP，在語義解釋(模型)的基礎上，可以證明系統IPN的可靠性和完全性，系統IPN還是能行可判定的 。
合取式
合取式是由合取詞聯結兩個公式構成的真值形式。如p∧q、 (p∨q) ∧r、(p→q) ∧ (⌝p→ ⌝q) 等等。 有時也特 指由合取詞聯結兩個命題變元構成的基本真值形式，即p∧q (讀作“p合取q”，或“p並且q”)。合取式與其合取支 (即由合取詞聯結的兩個公式) 之間的真值關係，可用p∧q的真值表來表示(以“T”表示 真，以“F” 表示假) ：
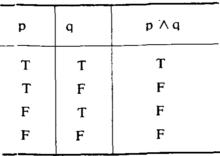合取消去規則此表說明，當p和q皆真時，p∧q為真; 當p和q中有一假或兩者皆假時，p∧q為假。用任一其他公式代替命題變元p或q，並不會改變這種真值關係。合取式是聯言命題的真值形式，它捨去了聯言命題的支命題之間在內容、意義上的聯繫。一個合取式的兩個合取支可互換位置，而並不改變該合取式的真值。但用日常語言表達的聯言命題，其支命題的前後順序往往是不能隨意顛倒的 。
