概述
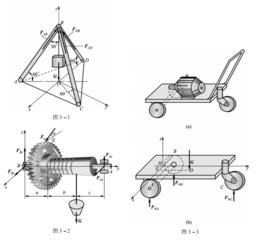
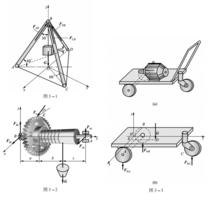
空間力各個力的作用線都不在同一平面內的力系稱為 空間力系 。 在空間力系中，若各個力的作用線匯交於一點， 則稱為空間匯交力系， 如圖 3-1 所示， 三角吊架的三根桿均為二力桿，其受力和物重 G 都匯交於球鉸 B 處構成一空間匯交力系； 若各個力的作用線在空間任意分布， 則稱為空間任意力系， 如圖 3 －2 所示， 起重絞車鼓輪的受力情況； 若各個力的作用線互相平行，則稱為空間平行力系， 如圖 3 －3 所示， 三輪推車的受力構成空間平行力系
力在空間直角坐標軸上的投影和力對軸之矩
力在空間直角坐標軸上的投影
1 直接投影法
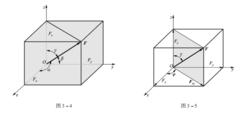
如圖 3 －4 所示， 已知力 F 的大小， 力 F 的作用線與空間直角坐標系三個坐標軸正向的夾角分別為 α、 β、 γ， 由幾何關係可直接得到力 F 在空間直角坐標軸上的投影 Fx、 Fy、 Fz 分別為
空間力式中的三個投影都是代數量， 與平面情況相同， 規定 當力的起點投影至終點投影的連線方向與 坐標軸正向一致時取正號； 反之， 取負號。 如果力 F 的三個投影是已知的， 則可以反求力 F 的大小與方向。 為此， 把式 （3 －1） 的每一個等式分別平方相加， 並注意到
空間力得
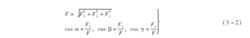空間力cos α， cos β， cos γ稱為力 F 的方向餘弦。
空間力2 二次投影法
如圖 3 －5 所示， 若已知力 F 的大小、 F 的作用線與坐標軸 z 的夾角 γ、 力 F 與 z 軸決定的平面與 x 軸的夾角為 φ， 則可先將力 F 分別投影至 z 軸和坐標平面 Oxy 上， 得到 z 軸上的投影 Fz 和平面上的投影 Fxy； 然後， 再將 Fxy分別投影至 x 軸和 y 軸， 得到軸上的投影 Fx、 Fy。 此方法需要經過兩次投影才能得到結果， 因此， 稱為 二次投影法 。 二次投影法的過程可參看下式：
空間力其中， γ為力 F 與 z 軸所夾的銳角， φ為力 F 與 z 軸所確定的平面與 x 軸所夾的銳角。 當力的起點投影至終點投影的連線方向與坐標軸正向一致時取正號； 反之， 取負號。注意： 力在軸上的投影是代數量， 而力在平面上的投影為矢量。 這是因為力在平面上投影的方向不能像在軸上的投影那樣簡單地用正負號來表明， 而必須用矢量來表示。
力對軸的矩
1 力對軸之矩的概念
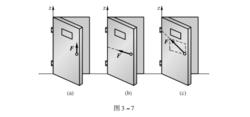
在工程實際中經常遇到剛體繞定軸轉動的情形， 如齒輪、帶輪等。為了度量力對繞定軸轉動剛體的轉動效應， 必須引入力對軸之矩的概念。 例如， 在推門時， 若力的作用線與門的轉軸平行或相交， 如圖 3 －7 所示， 則無論力有多大都不能把門推開。 當力垂直於門而不通過門軸時， 就能把門推開，而且這個力越大或其作用線與門軸間的距離越大， 則轉動效果就越顯著。 因此，可以用力 F 的大小與距軸的距離 d 的乘積來量度力 F 對剛體繞定軸轉動效應。
空間力如圖 3 －8 所示， 在門上 A 點作用任一空間力 F， 現過 A 點作一垂直於 z 軸的平面 β， 與 z軸交於點 O。 將力 F 分解為平行於 z 軸的分力 Fz 和垂直於 z 軸的分力 Fxy。 顯然， 分力 Fz 對門無轉動效應， 只有分力 Fx y才能使門轉動， 其轉動效應取決於力 Fxy 對 O 點的矩。 因此， 得到力對軸之矩的概念， 即 力對軸之矩是力使物體繞軸轉動效應的度量， 它是代數量， 其大小等於力在垂直於該軸的平面上的分力對於此平面與該軸交點之矩 ， 也即
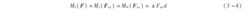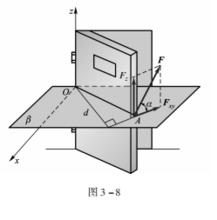空間力
空間力其正負號可用右手規則來確定： 以右手的四指指向符合力矩轉向而握拳時， 若大拇指指向與該軸的正向一致時取正號， 反之取負號 。通過以上分析可知， 力對軸的矩等於零的兩種情況是：
（1） 力與軸平行 （Fxy =0） ；
（2） 力與軸相交 （d =0） 。
也就是說力與軸在同一平面內時， 力對軸之矩為零。力對軸之矩的單位為 N· m。
2 合力矩定理
與平面力系合力矩定理類似， 空間力系的合力矩定理為： 空間力系的合力對某軸之矩， 等於力系中各分力對同一軸之矩的代數和， 即
空間力在實際計算力對軸之矩時， 套用合力矩定理往往比較方便。 具體方法是： 先將力 F 沿所取坐標軸 x、 y、 z 分解， 得到 Fx、 Fy、 Fz 三個分力， 然後計算每一分力對某軸 （如 z 軸） 之矩， 最後求其代數和， 即得出力 F 對該軸之矩， 即
Mz （F） =Mz （Fx） +Mz （Fy） +Mz （Fz）
由於 Fz 與 z 軸平行， Mz （Fz） =0， 可得
空間力空間力系的簡化與平衡
空間力系的簡化
與平面任意力系相同， 可依據力的平移定理， 將空間力系向任意點 O （簡化中心） 平移， 簡化為一個空間匯交力系和一個空間力偶系， 進而合成為一個主矢 FR′和一個主矩 MO 。 由於空間力系的各個力的作用線不在同一平面內， 當力平移時其附加力偶的作用面也不在同一平面內， 所以附加力偶矩必須用矢量表示， 故其主矩也為矢量。 由於空間力系的簡化過程較為複雜也超出了本書要求範圍， 這裡不作具體介紹， 只給出主矢 F′R和主矩 MO 的大小和方向餘弦的解析表達式。
（1）暢主矢FR′的大小和方向餘弦
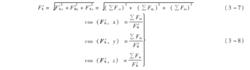空間力（2）暢主矩 MO 的大小和方向餘弦
空間力空間力系的平衡
（1） 空間力系 平衡的充分與必要條件是： 力系的主矢和對任一點的主矩都等於零 。 即
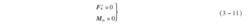空間力（2） 空間力系平衡方程 將式 （3 －7） 和式 （3 －9） 代入平衡條件式 （3 －11） 得解析式為
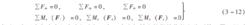空間力上式表示：力系中各力在任意空間坐標系每一個坐標軸上投影的代數和分別等於零 ； 同時
各力對每一個坐標軸之矩的代數和也分別等於零 。式 （3 －12） 稱為空間任意力系的平衡方程， 其中包含三個投影式和三個力矩式， 共有六個獨立的平衡方程， 因此可以解出六個未知量。
空間任意力系平衡問題的平面解法
對於空間力系的平衡問題， 可以直接運用平衡方程 （3 －12） 來解， 也可以將空間力系分別投影到三個坐標平面上， 轉化為三個平面任意力系， 分別建立它們的平衡方程來解。 這種將空間問題分散轉化為三個平面問題的討論方法， 稱為空間力系的平面解法。 機械工程中， 尤其是對輪軸類零件進行受力分析時常用此方法 。
