簡介
可解解變異外，總變異的剩餘部分被稱為未解釋變異（unexplained variation）或殘差（residual）。
線性回歸中的決定係數即為可解釋變異占總變異的比率。
變異
變異又可理解為 離散程度。
在統計學裡， 離散程度（ dispersion）是指一個分布壓縮和拉伸的程度。離散程度主要有方差、標準差和四分位距等。
離散程度與位置或者集中趨勢相對。
方差
方差（ Variance），套用數學裡的專有名詞。在機率論和統計學中，一個隨機變數的 方差描述的是它的離散程度，也就是該變數離其期望值的距離。一個實隨機變數的方差也稱為它的二階矩或二階中心動差，恰巧也是它的二階累積量。這裡把複雜說白了，就是將各個誤差將之平方（而非取絕對值，使之肯定為正數），相加之後再除以總數，透過這樣的方式來算出各個數據分布、零散（相對中心點）的程度。繼續延伸的話，方差的算術平方根稱為該隨機變數的 標準差（此為相對各個數據點間）。
標準差
標準差（又稱標準偏差、均方差，英語： Standard Deviation，縮寫 SD），數學符號 σ（sigma），在機率統計中最常使用作為測量一組數值的離散程度之用。標準差定義：為方差開算術平方根，反映組內個體間的離散程度；標準差與期望值之比為標準離差率。
四分位距
可解釋變異四分位距（interquartile range, IQR）。是描述統計學中的一種方法，以確定第三四分位數和第一四分位數的分別（即的差距）。與變異數、標準差一樣，表示統計資料中各變數分散情形，但四分差更多為一種穩健統計（robust statistic）。
決定係數
決定係數（英語：coefficient of determination，記為 R或 r）在統計學中用於度量因變數的變異中可由自變數解釋部分所占的比例，以此來判斷統計模型的解釋力。
對於簡單線性回歸而言，決定係數為樣本相關係數的平方。當加入其他回歸自變數後，決定係數相應地變為多重相關係數的平方。
假設一數據集包括 y,..., y共 n個觀察值，相對應的模型預測值分別為 f,..., f。定義殘差 e= y− f，平均觀察值為
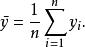可解釋變異於是可以得到總平方和
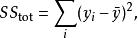可解釋變異回歸平方和
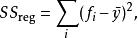可解釋變異殘差平方和
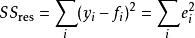可解釋變異由此，決定係數可定義為
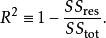可解釋變異