可加季節模型

由時間序列趨勢、季節因素和不規則因素組成的模型時間序列加法模型。不規則因素通常為不相關的，並且是獨立同分布的稱為可加季節模型。

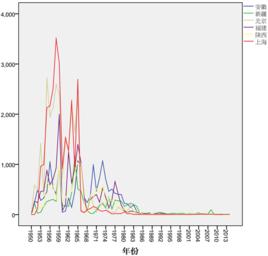
理論

如果我們不僅僅滿足予分解現有的時間序列，而且想要對未來進行預測，就需要建立模型。首先。這裡介紹比較簡單的指數平滑(exponential smoothing)。指數平滑只能用於純粹時間序列的情況，而不能用於含有獨立變數時間序列的考察變數之間關係的研究。指數平滑的原理為：當利用過去觀測值的加權平均來預測未來的觀測值時(這個過程稱為平滑)，離得越近的觀測值要給以更多的權。而“指數”意味著：按照已有觀測值“陳舊”程度增加的方向，在其上所加的權數按指數速度遞減。以簡單的沒有趨勢和沒有季節成分的純粹時間序列為例，指數平滑在數學上實際是一個幾何級數。這時，如果用K表示在I時間的平滑後的數據(或預測值)，那么指數平滑模型為

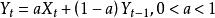可加季節模型

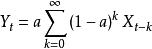可加季節模型

上面的公式是最簡單的指數平滑形式，無法應對具有各種成分的複雜情況。針對各種成分的情況有各種實用的指數平滑模型公式。

公式

我們根據數據，可以得到這些模型參數的估計以及對未來的預測。下面給出各種實用的指數平滑模型的公式。

對於時間序列X，趨勢、光滑後的序列、季節因子分別用T、S、I表示；另外，p表示周期，e為殘差。  

幾種指數平滑模型如下：

(1)線性趨勢可加季節模型(1inear trend，additive seasonality model)為

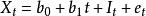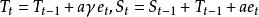可加季節模型

可加季節模型

可加季節模型

(2)指數趨勢可加季節模(exponential trend，additive seasonality model)為

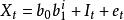可加季節模型

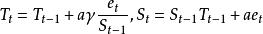可加季節模型

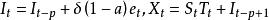可加季節模型

相關概念

指數平滑：指數平滑法是在加權移動平均法基礎上改進而來的一種廣泛使用的統計分析方法。它通過計算一系列指數平滑值來消除不規則變動，以反映時間序列的長期趨勢。指數平滑法既是對時間序列進行修勻的一種方法，也可以直接用於預測，還可以用於估計預測模型的參數。