反覆試驗法

什麼是反覆試驗法

從生產運作方面考慮，有三種純策略來處理非均勻需求：改變庫存水平、改變職工的數量和改變生產率(Production rate)。三種純策略可以任意組合成無數混合策略。比如，可以將改變工人的數量與改變庫存水平結合起來。混合策略一般要比純策略效果好。究竟採用什麼樣的策略，一般要通過反覆試驗。

反覆試驗法舉例

以一個例子說明如何套用反覆試驗法：
某公司將預測的市場需求轉化為生產需求，如表7-4所示。該產品每件需20小時加工，工人每天工作8小時。招收工人需廣告費、考試費和培養費，折合雇一個工人需300元，裁減一個工人需付解僱費200元。假設生產中無廢品和返工。為了應付需求波動，有1000件產品作為安全庫存。單位維持庫存費為6 元/件.月。設每年的需求類型相同。因此在計畫年度開始時的工人數等於計畫年度結束時的工人數。相應地，庫存量也近似相等。現比較以下不同的策略下的費用。

預測的需求

月份	預計月生產需求量(件)	累計需求量(件)	每月正常工作日數(天)	累計正常工作日數(天
4	1600	1600	21	21
5	1400	3000	22	43
6	1200	4200	22	65
7	1000	5200	21	86
8	1500	6700	23	109
9	2000	8700	21	130
10	2500	11200	21	151
11	250	13700	20	171
12	3000	16700	20	191

1	3000	197000	20	211
2	2500	222000	19	232
3	2000	242000	22	250

　1、僅改變工人的數量　採取這種純策略需假定隨時可以僱到工人，這種策略可見下表，總費用為200,000元。維持1000件安全庫存需1000×6×12=72,000元。總費用 128,000+72,000 = 200,000 元。

僅改變工人的數量

月份	預計月生產 需求量(件)	累計需求量 (件)20×(2)	每月正常 工作日數(天)	每人每月生產 小時8×(4)	需工人數 (3)/(5)	月初增加 工人數	月初裁減 工人數	變更費 300×(7) 或200×(8)
4	1600	32000	21	168	190		67	7400
5	1400	28000	22	176	159		31	6200
6	1200	24000	22	176	136		23	4600
7	1000	20000	21	168	119		17	3400
8	1500	30000	23	184	163	44		13200
9	2000	40000	21	168	238	75		22500
10	2500	50000	21	168	298	60		1800
11	2500	50000	20	160	313	15		4500
12	3000	60000	20	160	375	62		18600

1	3000	60000	20	160	375			0
2	2500	50000	19	152	329		46	9200
3	2000	40000	22	176	227		102	20400
合計						256	256	128000

　2、僅改變庫存水平 這種策略需允許晚交貨。由於252天內需生產24200件產品，則平均每個工作日生96.03件，需96.03×20=1920.63小時，每天需工人1920.63÷8=240. 08人。取241人，則每天平均生產241×8÷20=96.4件產品。僅改變庫存水平的策略如下表所示。總費用為209,253元。

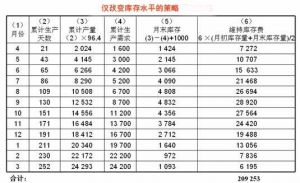僅改變庫存水平的策略.jpg

3、一種混合策略　混合策略可以多種多樣。考慮到需求的變化，在前一段時間採取相對低的均勻生產率，在後一段時間採取相對高的均勻生產率。生產率的改變不是通過加班加點，而是通過變更工人的數量。4月初需生產1600件，每天需生產76.19件。設前一段時間採用每天80件的生產率，則每天需80×20÷8=200工人。生產到8月底，累計109天生產了109×80=8720件。在餘下(252-109)＝143天內。要生產 (24200-8720)＝15480件產品，平均每天生產15480÷143=108.25件，需108.25×20÷8=270.6人，取271人。因此，9月初要雇71人，每天可生產271×8÷20=108.4件產品。年末再裁減71人。這種混合策略的總費用為179,275元

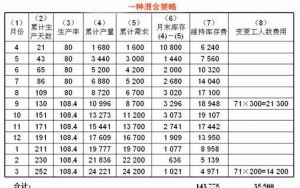混合策略.jpg