發現
用勺子舀出一勺蜂蜜，停在麵包上方幾厘米的地方，然後將勺子傾斜，讓蜂蜜緩慢下落，形成一股向下流動的細流，並落到麵包片上。蜂蜜沒有馬上鋪散開，而是堆積成一個螺旋狀的結構，類似一堆盤繞的繩索。上世紀50年代末，美國人喬治·巴恩斯(Barnes)和理察·伍德科克(Woodcock)注意到這種現象，將其命名為“卷繩效應”。
實驗
設計
矽油比蜂蜜的粘度變化範圍更寬，粘度是內部摩擦力抵抗流動變形的能力，粘度越大，流體自由流動就越困難。通過實驗設備，控制具體的流動條件(比如流體下落的速率和高度)，並觀察這些條件對盤繞頻率 (液體流盤繞一圈的快慢)的影響。
分析
對於流體液柱上的任何一段，主要受到兩種力的作用：向下的重力和流體內部的粘滯力(或摩擦力)。液柱有三種形變方式：拉伸、彎曲和扭曲。對於每一種形變，也都有一種與之對抗的粘滯力。液柱的形狀取決於所有這些力的相對大小以及流體的慣性(即質量乘以加速度)。
定義變數
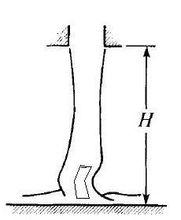
上方較長的為尾部(Tail)，下方較短的盤卷部分為卷繩(Coil)，尾部和卷繩的總高度計為H。重力加速度計為g
流體材料的流速計為Q，尾部的頂部半徑計為a0，尾部的底部半徑計為a1，卷繩的繞線角頻率計為Ω。
流體：密度計為ρ，表面張力係數計為γ，運動粘度計為v。
過程
一次實驗裡使用了高粘度(30 000 cSt)矽油，設定較高的流動速率(每秒0.14毫升)和較低的下落高度(3~4厘米)，結果偶然得到了這個總是有5條旋臂的星系狀結構。之所以會形成這種結構，是因為卷繩的中心並不固定，而是沿一個圓形軌道轉動。因此，卷繩螺旋部分相鄰的兩環會互相擠壓，在交叉區域形成許多氣泡。交叉點的位置緩慢沿圓形軌道移動，與此同時，氣泡隨著向四周擴散的流體也向各個方向散開。在這兩種運動的共同作用下，形成了氣泡螺旋波紋。但這種現象只在很小的粘度、流動速率和下落高度範圍內才會出現。
用粘度低得多的矽油進行了實驗。結果發現，它們的盤繞頻率最高可達每秒2 000圈，並且會以更加複雜的方式來盤繞甚至“摺疊”。如果沒有外界干擾，它們會一直保持一種盤繞狀態，但如果用指節大力敲擊一些實驗儀器，流體可能會馬上切換到另一種狀態。
在上述所有實驗中，流體下方的界面都是靜止不動的。但如果流體與界面之間存在相對運動又會出現一些新奇的現象。一種名為“流體縫紉機”的設備會通過噴口擠出粘性液體，落在下方勻速行進的水平傳送帶上。當傳送帶行進速度較快時，流體細線在傳送帶上留下一條筆直的跡線。但隨著速度減慢，會出現一些不穩定的複雜圖案，比如曲折蜿蜒的圖案，交替的圓圈圖案，雙螺旋甚至W形圖案。
結果
1.根據重力、慣性力和摩擦力三種力之間不同的平衡情況，下落的粘性流體會出現4種不同的盤繞形態：
卷繩效應
卷繩效應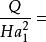
卷繩效應a 粘性模式(Viscous Regime)。當下落高度較低時——4~8毫米——“液繩”好像緩慢擠出的牙膏。流體盤繞的速度如此之慢，以至於相比於粘滯力，重力和慣性力都可以忽略不計。公式：Ω
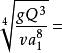卷繩效應
卷繩效應b 重力模式(Gravitational Regime)。當高度在1.5~7厘米之間時，重力開始成為影響因素。流體卷繩由兩部分組成：上方較長的尾部，以及下方較短的盤卷部分。在尾部，重力與抵抗拉伸的粘滯力相平衡。在盤卷部分，重力則與抵抗彎曲的粘滯力相平衡。尾部受力平衡，使得長尾部分看起來好像一條被底部螺旋部分斜拉著的鎖鏈。公式：Ω
卷繩效應
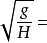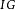卷繩效應
卷繩效應c 鐘擺模式(Inertio-Gravitatioval Regime)。當高度在7~12厘米之間時，尾部會像鐘擺一樣前後擺動。在大部分高度範圍內，尾部無法自由擺動，因為它實際上是隨著底部流體細流的盤繞而擺動的。但在某些高度，盤繞頻率與尾部的自然擺動頻率恰好相符，在這種正反饋情況下會發生共振。於是，尾部開始繞一個大圓旋轉。公式：Ω
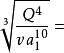卷繩效應
卷繩效應d 慣性模式(Inertal Regime)。當高度大於15厘米時，尾部幾乎完全垂直，因為底部的螺旋結構無法再給它施加足夠大的側向拉力。在螺旋結構內部，抵抗彎曲的粘滯力幾乎完全被慣性力平衡，重力只扮演次要角色。公式：Ω
2.相比於粘稠的流體，流動性更強的液體可不僅僅只會形成盤繞結構而已。
下面這些例子裡，使用了粘度在400~6 000 cSt的矽油——比蜂蜜更稀，但比水更稠。
卷繩效應a 滯留。當流體粘度較低、下落高度較低、流動速率較高時，流體垂直下落，在金屬板上向四周均勻擴散。生活中常見的流體，比如水和橄欖油，也會這樣。但如果條件恰當，這些流體也可以形成盤繞結構。比如，讓橄欖油從10厘米的高處以每40分鐘1毫升的速度向下滴落，卷繩現象就會出現。
b 旋轉摺疊。“液繩”會周期性的自我摺疊。同時，整個摺疊結構會繞一垂直軸旋轉，產生某種扭曲效果。
卷繩效應c 超纏繞。超纏繞是形容纏在一起的電話線的一種專業說法，指在電話線已有緊密纏繞的結構上進行大的二次纏繞。對流體而言，下落的液流堆積成一個中空的圓柱結構，構成主盤卷，而圓柱結構還從整體上再次進行二次盤卷。二次盤卷的速度比較緩慢，只有主盤卷的十分之一。
詳解
由於內部摩擦力是分子間作用力導致下面一律改用吸引力和排斥力。
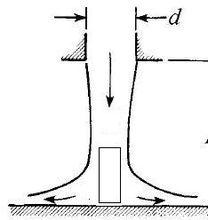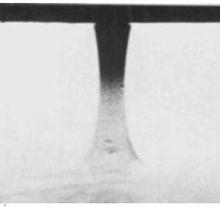
卷繩效應左邊的圖像，描述的是流體流到平面上鋪散的情形。像水這種粘度很小的液體，因為水分子之間的吸引力很小，鋪散過程非常迅速。
但是黏稠的液體，分子之間的吸引力較大，鋪散的過程就會慢一些。這導致長方形區域的液體還來不及向四周流逸，而新的液體柱又流了下來。這樣，就會有一部分液體堆積在一起，形成一個類似圓柱一樣的結構。
很明顯，這個液體圓柱的結構不是靜態的。雖然底層以及最外層的液體會不斷流失，看起來像是坍塌一樣，但是上方不斷有新的液體流下來補充，這個圓柱形的累積液柱在動態中得以保持。在動態的平衡中，液體圓柱內部分子之間的引力，對抗圓柱本身的重力以及慣性。如果兩者之間的力量能保持平衡，液體柱的形態就會以上圖表現出來的形式穩定下去。
所以當我們開始向手上傾倒香波的時候，香波就會如圖所示的樣子靜靜的流淌。
當我們將香波瓶子提高一點，讓香波從更高處流出，情況就有了變化。香波液流的長度增加，由於重力加速度，越到下方，液體的直徑越小，速度越大。
回到上面的圖，可以看到，中心的圓柱受到的來自重力以及慣性的壓力在增加，而圓柱的直徑在減小。一旦圓柱的分子間吸引力不足以平衡重力及慣性，這個柱子就會坍塌（failure）。
一根不堪重負的柱子，會產生什麼樣的變化？右圖是它受力時候發生的兩種情況。
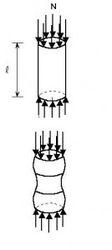先上面後下面，直徑變化很小可以忽略如果這根柱子內部的分子，是完全一樣的，柱子的任意水平切面上，所有的分子受力情況都相同，這根柱子就會像右圖所示那樣壓縮變形（crushing）。兩端所受到的壓力，將使得這跟柱子產生外形的變化（形變），同時在垂直方向上，內部分子之間因為距離縮短，表現為相互排斥，並積蓄勢能。
但是如果情況不是這樣，柱子將會發生什麼變化呢？
卷繩效應肯定有同學玩過左邊這個疊木塊的遊戲。在這個遊戲中，兩個玩家依次從這個木塔中部取出一根木塊，最後誰導致木塔的倒塌，誰就是輸家。整個木塔的重心，保持在中心縱軸上。在某水平切面上，如果和中心縱軸等距離的某處的受力，和其他對稱位置的受力相比，出現足夠大的差異，木塔的重心偏離中心縱軸，木塔就會倒塌。
剛性材料受力過程中發生的折彎（buckling），和這種現象有共通之處。
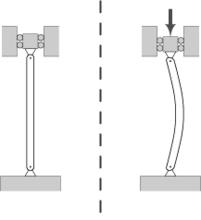卷繩效應左邊是一根桿狀材料，在受力之下發生折彎的情景。為什麼剛才說柱子受力會發生壓縮，這裡的桿卻折彎呢？其實如果桿內部物質分布足夠均勻，使得內部力的分布足夠均衡，材料本身的形態也對稱，則只會發生壓縮（crushing），不會發生（buckling）。
可是自然界的物質，幾乎就沒有完全均質的。難道說折彎(buckling)必然會發生？
也不是這樣。只有當材料的長度直徑比（slenderness ratio）達到某一個水平，或者材料內部物質分布的不均勻達到一個程度，應力在中部集中，其受力分布的異常程度能克服材料邊界的限制，突破邊界的折彎才會發生。
卷繩效應流體的液柱，是由一個動態的平衡過程來保持其形態穩定的。在物質不斷更換的過程里，總會有局部的異常形態出現。有時候是一個氣泡，有時候是一個密度較小的團塊，有時候是什麼別的因素。這種內在的異常，破壞了液體內部分子間的引力和液柱重力以及慣性之間的平衡。當這種不平衡的狀態，嚴重到一定的程度，就會導致彎折的發生。如右圖。
卷繩效應原本處於壓縮狀態下的某部分物質，受到側方向的推擠，向阻力最小的方向釋放勢能，先加速後減速遠離中心軸，分子間的壓力隨著離開中軸越來越遠，漸漸轉變成分子間拉力，這股力量同時也作用在即將落下的液體。在重力和慣性協同作用下，液柱向反方向開始新一輪的彎折。最下層的液柱，在往復過程中，內部分子在受壓－牽拉兩種狀態之間來迴轉換，形成振動。表現為在原位的往復。以時間為橫軸，振幅為縱軸的話，形成左圖所示的波動。
左邊長軸，右邊短軸左面這兩張相片，描繪的就是上文中所說的情形。只是我們先看看這個過程發生在一個平面：一道扁平的液柱流淌下來，在長軸方向上，儘管有內部的不均衡存在，但是這種不均衡無法突破較寬的邊界限制，更多地表現為壓縮形變（crushing），即寬度默認不變，而在短軸方向上，內部不均衡易於突破較窄的邊界限制，表現為彎折，形成振動。
正像我們前面說到的，儘管上面這個實驗中長軸具有較寬的邊界，這個障礙也是相對的。一旦液體的黏稠度足夠大，下落的距離足夠高，即使是這樣的寬度，仍然會形成彎折，產生振動。
當我們將液柱的扁平形態變成最常見的圓柱形，我們所觀察到的過程將不限於一個平面內，變得有點複雜，但是本質保持不變。
卷繩效應黏液下落過程中形成的液柱內部，因為局部的不均衡受力，導致液柱向某一個方向彎折，形成最初的振動。
這個振動是在某一個平面內產生的。就像左上圖所示。但在和這個平面垂直的方向看，則沒有振動發生，只是壓縮形變。就像在右邊圖片中所看到的。
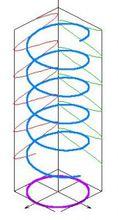
卷繩效應在這個平面上，一旦有新的因素，誘發在這個平面內發生彎折，就會出現另外一個波動。
兩者所在的平面相互垂直。前後兩種振動疊加，形成三維振動。如左圖。
實際上，這兩個過程並不是這么截然分開，兩個平面內的振動，一起影響這條液柱的運動形態。各自條件不同，兩個振動的振幅、頻率也不同，產生出來的綜合形態也不同。因此在平面上產生的堆積形變可表現為單純的摺疊（folding），也可表現為花瓣型，也可表現為8字型（figure of eight）。
當兩個平面內的振幅以及頻率趨於一致，堆積則表現為螺旋狀，卷繩效應產生。
現 在，這種現象大部分決定性因素已經得以釐清。卷繩效應的頻率、振幅、卷繩的直徑、黏液的邊界高度、邊界黏稠度以及螺旋堆積能達到的高度，都被計算出來了。
性質
對於不同盤繞形態的實驗發現：
（1）流動速率較低時，流體下落高度越高，盤繞頻率越低
（2）流動速率較高時，流體下落高度越高，盤繞頻率越高
（3）當下落高度固定在某個特定值時，流體卷繩會在兩個不同盤繞頻率間隨機切換
套用
矽油塑像：
矽油等粘性流體落在下方物體表面時，會自發出現盤繞現象。如果速度足夠快，會堆積成一個中空的圓柱結構。圓柱不斷增高，高度達到某個臨界值會發生坍塌，整個過程有重新開始，如此循環往復。
