正文
自有史以來可分為三個時期：①在吠陀(Vedic)期前期,約從公元前十世紀到公元前六世紀。使用曆法的曆日制度很不一致。有以12個恆星月為一年，一恆星月27日，一年324日;有以13個恆星月為一年，一年351日；有以12個朔望月為一年，6個大月，每月30日，6個小月,每月29日,一年共354日；有以360日為一年，稱作一世間年，每年分作12個月,每月30日，稱為世間月；有以“假設”太陽年為378日,即以一世間年加18日。過兩個世間年之後接一個“假設”太陽年,實際上是一年為366日。這樣的年可稱之為太陽年。②吠陀期後期，約公元前六世紀到公元後二世紀。這時期內有耆那(Jaina)歷。這個曆法以一星宿年=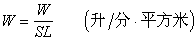
日，一太陰年=日，一世間年=360日，一太陽年=366日。凡五個太陽年(一瑜伽，yuga)有60個太陽月(Solar month)，61個世間月(karmamonth)，62個朔望月(lunar month)，67個星宿月(naksatra month)。由此可以推算出一太陽月=日，一世間月=30日,一朔望月=日，一星宿月=日。這樣，一個有閏月的太陰年=日。這些數據和名稱在唐代即已傳入中國。 當時編的《法苑珠林》卷七中已有著錄。其中把太陽月譯成日月，朔望月譯成月月。書中還有推入日季日數和月季日數的方法。 所謂日季是兩個太陽月， 即日;所謂月季是指一星宿月的六分之一，即一個月季=日③悉檀多 (Siddhanta)時期，約自公元三世紀到十二世紀。悉檀多指曆法的總名，意譯為“曆數書”。至於悉檀多的注釋工作，到公元十八世紀還沒有停止過。這時期的曆法很多，其中有代表性的是《五大曆數全書彙編》 (Pancasiddhatika)中的各歷（以下簡稱《五》）、 傳到中國的《九執歷》（以下簡稱《九》）和婆羅門笈多 (Brahmagupta)撰的曆書（音譯為《乾陀乾迪迦》，意譯為《曆法甘露》，以下簡稱《甘》）。 設Y為積年，為閏周,b為一朔望月不足30日的差數,
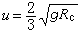式中x為一常數。在《五》、《九》中x=0，在《甘》中則
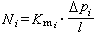又設m為其年曆過月數，d為其月曆過日數，則： 積月
積日(ahargana)
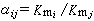
印度曆法中有三種上元:①上元自天地開闢算起。②上元自公元前3102年2月17日,星期五算起，這個曆元稱為卡利·尤幾(Kali yuge)。③以釋迦(Saka)紀年為上元，釋迦元年為公元78年(3 月15日)。釋迦元年離卡利·尤幾年數為:3102+(78-1)=3179。《五》歷從釋迦427年制呾邏月白半一日起算,故Y=3179+427=3606。《甘》歷從釋迦587年制呾邏月白半一日起算，故Y=3179+587=3766。
玄奘《大唐西域記》卷二《印度總述·歲時》條記錄了當時印度曆法。以時極短者叫剎那(ksana)，120剎那為一呾剎那(taksana)，60呾剎那為一臘縛(lava),30臘縛為一牟呼栗多(muhurta)，5牟呼栗多為一時,6時合成一日夜。月盈到滿叫白分(又叫白半，白博叉Paksha)，月虧到晦叫黑分（又叫黑半，黑博叉）。黑前白後，合為一月，12個月為一歲。各月的名稱是：閏月叫沙姆沙爾白(Samsarpa)，意思是偷偷進來的月。
