博雷爾代數
當X是一個度量空間時，博雷爾代數可以用如下生成的方法描述。
對於X的一族子集T（即X的冪集P(X)的任何子集），令
•T為T中元素的可數並的全體
•T為T中元素的可數交的全體
•T=(T).
現在利用超限歸納法定義如下的序列G，其中m是一個序數：
•對於初始的情況，定義
•G= X的所有開子集全體。
•如果i不是極限序數，那么i是i-1的後繼序數。令
•G= [G]
•如果i是極限序數，令
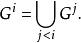博雷爾集我們現在可以說博雷爾代數是G，其中ω是第一不可數序數，即勢為ℵ₁的序數集。這意味著博雷爾代數可以通過開集全體的疊代運算
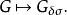博雷爾集至第一不可數序而生成。
為了證明這一點，首先注意到度量空間中的任何開集都是一列遞增緊集的並。特別地，易知對於任何極限序數m，集合的差運算將G映射到自身；而且，當m是不可數的極限序數時，G在可數並運算下是封閉的。
注意到對於每一個博雷爾集B，存在一個可數序數α使得B可以通過α多次疊代後得到。但是隨著B取遍所有博雷爾集，α也會相應地取遍所有可數序數，故而要得到所有博雷爾集所需的最靠前的序數是ω，即第一不可數序數。
例子
一個重要的例子，尤其是對於機率論而言，是實數集上的博雷爾代數。它是用來定義博雷爾測度的代數。對於機率空間上一個給定的實隨機變數，其機率分布按照定義，也是一個博雷爾代數上的測度。
實直線 R上的博雷爾代數是包含所有區間的最小σ-代數。
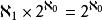博雷爾集在利用超限歸納法構造時，可以證明在每一步中，集合的數量至多是連續統的冪。所有博雷爾集的總數不會多於。
非博雷爾集
下面描述了盧津給出的一個實數集上的子集不是博雷爾集的例子。與之形成對比的是，不可測集的例子是無法給出的，不過其存在性是可以證明的。
每一個無理數都有一個唯一的連分數表示
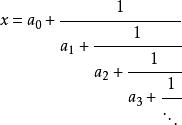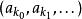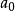博雷爾集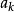
博雷爾集
博雷爾集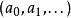
博雷爾集
博雷爾集其中是一個整數，其餘的都是正整數。令A為對應序列的無理數組成的集合，而且其中的元素滿足下列性質：存在一個無限子序列使得序列中每一個元素都是下一個元素的因子。這個集合A不是博雷爾集。事實上，這個集合是一個解析集，進一步地，在解析集全體構成的類中是完備的。
