負定矩陣是一種特殊的實對稱矩陣。對於負定實二次型的矩陣 A若實二次型是半負定的，則 f 的矩陣 A 稱為半負定的。
負定矩陣是一種特殊的實對稱矩陣。
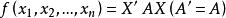半負定矩陣
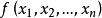半負定矩陣對於負定實二次型 的矩陣 A。若實二次型 是半負定的，則 f 的矩陣 A 稱為半負定的。
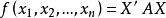半負定矩陣設 是實二次型，則下列的條件等價：
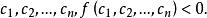半負定矩陣1、f 是負定的，即對於任意不全為零的實數組
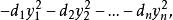半負定矩陣2、f 有標準形 而 d 全為正實數 (i=1,2,...,n).
3、f 的負慣性指數為 n.
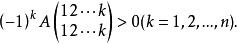半負定矩陣4、
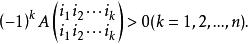半負定矩陣5、
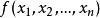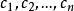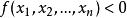半負定矩陣
半負定矩陣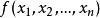
半負定矩陣 半負定矩陣設 是二次型，對於任意一組不全為 0 的實數 ，如果都有 ，那么 是負定的。
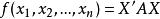半負定矩陣實對稱矩陣A是負定的，如果二次型 負定。
因為正定二次型與正定矩陣有密切的聯繫，所以在定義正定矩陣之前，讓我們先定義正定二次型:0。
定義 判別方法定型二次型是實二次型的類型。正定、半正定、負定、半負定的二次型合稱為定型二次型；不定的二次型稱為不定型二次型。
簡介 正定二次型在數學中，矩陣（Matrix）是一個按照長方陣列排列的複數或實數集合 ，最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提...
歷史 定義 基本運算 乘法 行列式在數學中，矩陣（Matrix）是一個按照長方陣列排列的複數或實數集合 ，最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提...
歷史 定義 基本運算 乘法 行列式半正定矩陣是正定矩陣的推廣。實對稱矩陣A稱為半正定的，如果二次型X'AX半正定，即對於任意不為0的實列向量X，都有X'AX≥0.
概述 性質 判定不定矩陣是一個數學術語，指的是如果一個埃爾米特矩陣既不是半正定也不是半負定的，那么稱其為不定矩陣。
正定矩陣的定義 負定、半定及不定矩陣 相關性質 非埃爾米特矩陣的情況 參見線性陣不等式被廣泛用來解決系統與控制中的一些問題，隨著求解線性矩陣不等式的內點法的提出、MATLAB 軟體中LMI 工具箱的推出，線性矩陣不等式這一工具...
定義 線性矩陣不等式的發展 可轉化為線性矩陣不等式表示的問題黑塞矩陣（Hessian Matrix），又譯作海森矩陣、海瑟矩陣、海塞矩陣等，是一個多元函式的二階偏導數構成的方陣，描述了函式的局部曲率。黑塞矩陣最早...
定義 對稱性 利用黑塞矩陣判定多元函式的極值線上性代數，特別是二次型理論中，常常用到矩陣間的契約關係。兩個矩陣A和B是契約的，若且唯若存在一個可逆矩陣 C，使得C^TAC=B，則稱方陣A契約於矩陣...
定義 性質 正定二次型 契約矩陣發展史