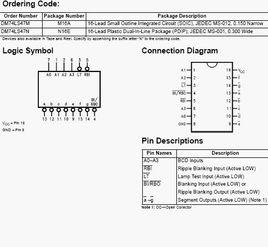
簡介
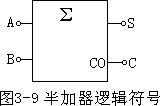半加器半加器是實現兩個一位二進制數加法運算的器件。它具有兩個輸入端(被加數A和加數B)及輸出端Y。
是數據輸入被加數A、加數B，數據輸出S和數(半加和)、進位C0。
A和B是相加的兩個數，S是半加和數，C是進位數。
所謂半加就是不考慮進位的加法，它的真值表如下 (見表)：
| 被加數A | 加數B | 和數S | 進位數C |
| 0 0 1 1 | 0 1 0 1 | 0 1 1 0 | 0 0 0 1 |
表中：
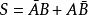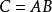半加器
半加器分析
由邏輯狀態表可寫出邏輯式，按組合數字電路的分析方法和步驟進行。
1．寫出輸出邏輯表達式
2．列出真值表
半加器的真值表見下表。表中兩個輸入是加數A0和B0，輸出有一個是和S0，另一個是進位C0。
| 輸入 | 輸出 | ||
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
3．給出邏輯說明
半加器是實現兩個一位二進制碼相加的電路，因此只能用於兩個二進制碼最低位的相加。
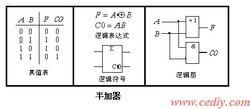半加器因為高位二進制碼相加時，有可能出現低位的進位，因此兩個加數相加時還要計算低位的進位，需要比半加器多進行一次相加運算。
能計算低位進位的兩個一位二進制碼的相加電路，即為全加器。
實現
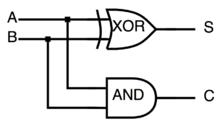半加器的邏輯實現半加器不考慮低位向本位的進位，因此它不屬於時序邏輯電路，有兩個輸入端和兩個輸出。
設加數（輸入端）為A、B ；和為S ；向高位的進位為Ci+1
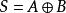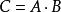半加器
半加器邏輯表達式：；。
輸入和輸出
半加器有兩個輸入和兩個輸出，輸入可以標識為A、B，輸出通常標識為求和（ Sum）和進位（ Carry）。輸入經異或（XOR）運算後即為S，經和（AND）運算後即為C。
半加器有兩個二進制的輸入，其將輸入的值相加，並輸出結果到和（ Sum）和進位（ Carry）。半加器雖能產生進位值，但半加器本身並不能處理進位值。
與全加器區別
半加器沒有接收進位的輸入端，全加器有進位輸入端，在將兩個多位二進制數相加時，除了最低位外，每一位都要考慮來自低位的進位，半加器則不用考慮，只需要考慮兩個輸入端相加即可。
