概念
電子計算機自誕生以來,其工作原理一直採用二進制形式,在日常中人們習慣於使用十進制數,在與二進制計算機進行人機對話時,機內需要將十進制與二進制之間反覆進行轉換,造成其資源浪費。因此,研製十進制計算機是必要的。
在十進制計算機中對機器數的定義與二進制機器數的定義類似,即將“+”、“-”符號數位化了的數據稱為機器數,而把它表示的值稱為機器數的“真值”。區別在於用“0”和“9”表示正號和負號,而後者則是用"0"和"1"表示正號和負號。機器數可用原碼、補碼和和反碼錶示。
定點表示
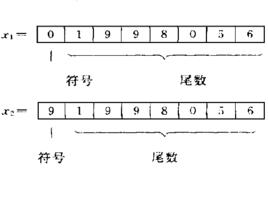
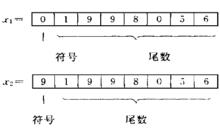 圖1 X1、X2的定點表示
圖1 X1、X2的定點表示在十進制計算機中,帶小數點的十進制數可以用定點表示,也可以用浮點表示。所謂定點表示,就是小數點在數中的位置是固定的;而浮點表示,小數點在數中的位置是浮動的。
對於任一個十進制數總可以表示為純小數或整數與一個10的整數次冪的乘積。例如十進制數X可寫成:
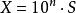 十進制反碼
十進制反碼其中,S稱為數X的尾數,n稱為數X的階碼。尾數S表示了數X的全部有效字,階碼n確定了小數點的位置。
假如n= 0,且尾數S為純小數,這時定點數只能表示小數;假如n= 0,且尾數S為純整數,這時定點數只能表示整數。
在十進制計算機中,數的正負符號也要用十進制數字來表示,採用其中哪兩個數字來表示數符,一般不能隨意,須採用“0”和“9”兩個數字來表示數符,`0’表示正號,`9’表示負號。
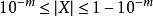 十進制反碼
十進制反碼例如:X1=+ 1998056, X2= -1998056,它們在計算機中的定點表示如圖1所示。最左邊的第一位為符號位,其餘各位為尾數位,m位尾數的定點機所有表示的數X的範圍為: 。
表示方法
十進制定點機器數表示方法
原碼錶示法
十進制定點整數的原碼錶示,即用機器數的最高位作為符號位,其餘各位給出數值的絕對值的表示方法,其定義是:
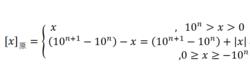 十進制反碼
十進制反碼其中,n為x的位數。
十進制定點小數的原碼錶示定義為:
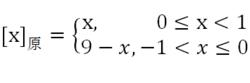 十進制反碼
十進制反碼例如,x=+ 0.1234,,[x]原= 01234;x=-0. 1234,[x]原= 91234。
反碼錶示法
十進制定點整數的反碼錶示,即用機器數的最高位作為符號位,數值為是對負數各位取反的表示方法,其定義是:
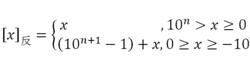 十進制反碼
十進制反碼十進制定點小數的反碼錶示定義為:
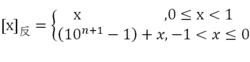 十進制反碼
十進制反碼其中,n為x的位數。
例如:X=+ 0. 1234,[X]反= 01234;X= -0. 1234,[X]反= 98765。
補碼錶示法
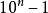 十進制反碼
十進制反碼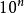 十進制反碼
十進制反碼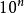 十進制反碼
十進制反碼模數:即計算器的容量(剛產生溢出時的溢出量),設十進制計數器為n位,則可以表示的數值範圍為0~ ,再加1則剛產生溢出,溢出量為 ,模數即為 。
十進制定點整數的補碼錶示,即用機器數的最高位作為符號位,其餘各位給出的數值按10取模的結果的表示方法,其定義是:
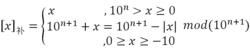 十進制反碼
十進制反碼十進制定點小數的反碼錶示定義為:
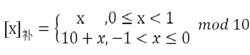 十進制反碼
十進制反碼其中,n為x的位數。
例如:X=+ 0. 1234, [X]補= 01234;X= -0. 1234,[X]補= 98766。
性質
(1) 當一個帶符號數用反碼錶示時,最高位為符號位, 0表示正號;,9表示負號。
(2) 0的反碼錶示有+0和-0之分,即[+0]反=00,[-0]反=99。
(3) 反碼參與運算時,符號位與其他數值位同等對待,且避免了補碼運算過程需做減法的不便。如:[2]反+[-9]反=02+90=92(真值為-7)。