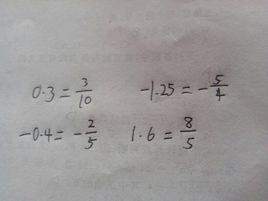定義
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 0 |
就是化分數的定義
有限小數化分數
小數化分數,小數點前不變,小數點後面有N位分子就乘以10的N次方,分母為10的N次方,然後約分化簡例如:1.5,就是1不變,0.5乘以10得5,分母為10,化簡後就是3/2,又如2.124,就是2不變,0.124乘以1000就是124,分母為1000,化間後為2又250分之31.其次要記住一些常量例如0.25=1/4,0.125=1/8,0.5=1/2,0.2=1/5,0.33…3=1/3等等
無限(循環)小數化分數
而無限小數又分無限循環小數和無限不循環小數,無限循環小數可以化成分數,而無限不循環小數屬於無理數,無法化成分數無限循環小數又分純無限循環小數(就是說,從十分位開始就是循環節,如0.12341234,其中1234為循環節)和混無限循環小數(就是說,十分位還不是循環節,如0.12333333,3為循環節)!!!!!註:在這裡,整數部分忽略不記,但在實際運算中必須加上;還有就是純無限循環小數&混無限循環小數,這裡“純”和“混”是加上去的,可能這種說法不正確,所以不要隨便說,但理解就好先說純無限循環小數,化成分數,分子就是循環節,而分母,就是循環節是N位,那分母就是N個9(這裡是說99999這樣連起來的自然數),如0.12341234,1234循環,循環節個數為4,那化成分數,就是分母為4個9,分子為循環節1234,即1234/9999再說混無限循環小數,化成分數,分子就是小數點後面的非循環節部分和一個循環節連起來的數減去非循環節部分,分母是循環節位數個9和非循環節位數個0連起來,如0.12333333,3循環,分子就是123-12=111,分母是900,即111/900