幾何學定義
在幾何學中,某個曲線族的包絡線(),是跟該。(曲線族即一些曲線的無窮集,它們有一些特定的關係。在力學中由多個極限莫爾應力圓所確定的岩石的應力應變關係的曲線,該包絡線形狀一般是拋物線型,也有人試驗得出包絡線是直線型。
)
一曲線族的包絡線是這樣的曲線:該曲線不包含於曲線族中,但過該曲線的每一點,都有曲線族中的一條曲線與它在這一點相切。
設一個曲線族的每條曲線Cs可表示為Ft(x,y,s)=0,其中s是曲線族的參數,t是特定曲線的參數。若包絡線存在,它是由得出,其中h(s)以以下的方程求得:
若曲線族以隱函式形式F(x,y,s) = 0 表示,其包絡線的隱方程,便是以下面兩個方程消去s得出:
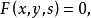 包絡線
包絡線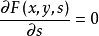 包絡線
包絡線繡曲線是包絡線的例子。直線族(A−s)x+sy= (A−s)(s)(其中A是常數,s是直線族的變數)的包絡線為拋物線。
電子信息學定義
一個高頻調幅信號,它幅度是按低頻調製信號變化的。如果把高頻調幅信號的峰點連線起來,就可以得到一個與低頻調製信號相對應的曲線。這條曲線就是包絡線。
經濟學定義
在經濟學上指的是每條包絡線上,在連續變化的每一個產量水平上,都存在著長期成本LTC曲線和一條短期成本STC曲線的相切點,該STC曲線所代表的生產規模就是生產該產量的最優生產規模,該切點所對應的總成本就是生產該產量的最低總成本。

