簡介
勒雷積分表示公式是一種多複變函數論的柯西型積分，即所謂勒雷積分表示公式。它是勒雷(Leray, J.)在很廣的條件下得到的，用它可導出最常用的柯西-凡塔皮耶積分表示公式。
定義
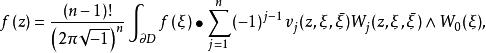勒雷積分表示公式
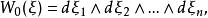勒雷積分表示公式
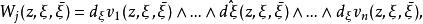勒雷積分表示公式
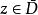勒雷積分表示公式
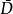勒雷積分表示公式由柯西-凡塔皮耶積分表示可以得出柯西-凡塔皮耶積分表示，又稱為勒雷積分表示公式： 其中 又f(z)在z∈D上全純，在 連續，這裡 為域的閉包。
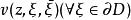勒雷積分表示公式最重要的柯西-凡塔皮耶公式還要求加上條件：向量函式 關於z全純。
柯西-凡塔皮耶積分表示
柯西-凡塔皮耶積分表示是重要的積分表示公式，它可推出許多已有的積分表示公式，當希洛夫邊界不是整個邊界時，和由華羅庚引進的柯西-賽格積分表示公式是兩種獨立的重要積分表示公式。
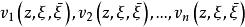勒雷積分表示公式柯西-凡塔皮耶積分表示的定義如下：設D為C中的有界域，它的邊界為逐塊光滑的。如果存在n個函式 它們關於z在D上連續，關於ξ在∂D上一階連續可微，且適合勒雷條件：
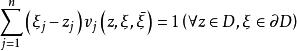勒雷積分表示公式1、 。
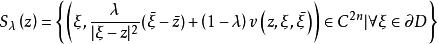勒雷積分表示公式
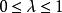勒雷積分表示公式
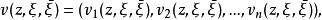勒雷積分表示公式
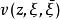勒雷積分表示公式
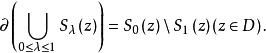勒雷積分表示公式2、任意取z∈D，則當ξ在∂D上變動時，做R中實超曲面簇 其中 ， 則向量函式 適合條件
