簡介
勒貝格外測度為定義點集的勒貝格測度而建立的預備性概念，簡記為(L)外測度。
外測度的概念是測度定義的基礎。
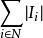勒貝格外測度對於R 中的任一點集E，把覆蓋E的可數個開區間的體積之和的下確界稱為E的勒貝格外測度，簡稱為E的外測度，記為m*(E)或|E|，即m*(E)=inf{|{I}為覆蓋E的可數個開區間}。
結論
在R 中，區間I的外測度等於它的體積，即m*I=|I|。
在R中，開集的外測度等於它的構成區間長度之和，並且對於R 中任意點集E它的外測度等於包含E的開集G的外測度的下確界，即m*(E)=inf{m*(G)|G是包含E的開集}。
性質
R 中點集的外測度具有下列基本性質：
1、非負性：m*(E)≥0，m*(∅)=0。
2、單調性：若E⊂E，則m*(E)≤m*(E)。
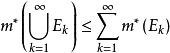勒貝格外測度3、次可加性：。
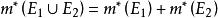勒貝格外測度4、若集E,E⊂R ，它們的距離ρ(E,E)>0，則。這是開集為可測集的基礎。
