介紹
數學上, 加托導數(英文: Gâteaux derivative)是微分學中的方嚮導數的概念的推廣。它以勒內·加託命名,他是一位法國數學家,年青時便死於第一次世界大戰。它定義於局部凸的拓撲向量空間上,可以和巴拿赫空間上的弗雷歇導數作對比。二者都經常用於形式化泛函導數的概念,常見於變分法和物理學,特別是量子場論。和其他形式的導數不同,加托導數是非線性的。
定義
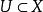 加托導數
加托導數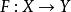 加托導數
加托導數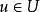 加托導數
加托導數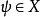 加托導數
加托導數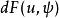 加托導數
加托導數假設 X和Y 是局部凸拓撲向量空間,(例如巴拿赫空間), 是開集合(open set),且 。F在點 沿著 方向的加托偏微分(Gâteaux differential) 定義為
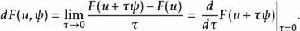 加托導數
加托導數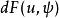 加托導數
加托導數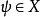 加托導數
加托導數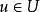 加托導數
加托導數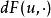 加托導數
加托導數如果極限存在。固定 u 若 對於所有 都存在,則稱F在 是加托可微(Gâteaux differentiable )。若F在u是加托可微,稱 為在u的加托導數。
稱F是在U中 連續可微的,若
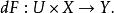 加托導數
加托導數是連續的。
屬性
若加托導數存在,則其為唯一。
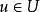 加托導數
加托導數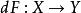 加托導數
加托導數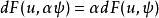 加托導數
加托導數對於每個 ,加托導數是一個運算元 。 該運算元是齊次的,使得 ,但是它通常不是可加的,並且,因此而不總是線性的,不像Fréchet導數。
例子
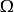 加托導數
加托導數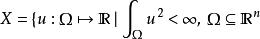 加托導數
加托導數 加托導數
加托導數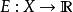 加托導數
加托導數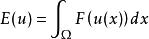 加托導數
加托導數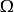 加托導數
加托導數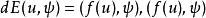 加托導數
加托導數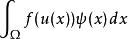 加托導數
加托導數令X為一個在歐幾里得空間勒貝格可測集上的平方可積函式的希爾伯特空間,也就是說 是勒貝格可測集 。泛函 由 給出,其中 F 是一個定義在實數上的可微實值函式且F'=f而u為定義在 的實數值函式,則加托微分為 為內積形式,其積分形式為 。
更詳細的說:
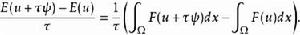 加托導數
加托導數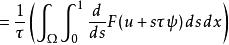 加托導數
加托導數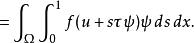 加托導數
加托導數 加托導數
加托導數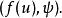 加托導數
加托導數令 (並假設所有積分有定義),得到內積 :
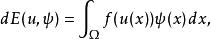 加托導數
加托導數上式表達式稱為泛函 E在 u( x)處關於增量 ψ的加托微分,其中 f( u(x))為泛函 E在 u( x)處的加托導數。
參看
•導數 (推廣)
