定義
 創造集
創造集 創造集
創造集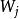 創造集
創造集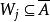 創造集
創造集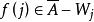 創造集
創造集 創造集
創造集定義1設 是一個遞歸可枚舉集。若存在遞歸函式 使對任何遞歸可枚舉集 ,如果 , ,就說 是 創造集。
與創造集緊密聯繫的有另一個概念,即生產集。
 創造集
創造集 創造集
創造集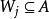 創造集
創造集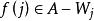 創造集
創造集 創造集
創造集定義2給定集合 ,若存在遞歸函式 ,使當 時, ,就說A是一個 生產集, 叫A的 生產函式。
生產集當然不是遞歸可枚舉集。
定義3利用生產集的概念,可以重新定義創造集如下:
若A滿足下列條件:
(1) A 是遞歸可枚舉集;
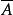 創造集
創造集(2) 是生產集,
就說A是創造集。
生產集的特點是從它的任何一個遞歸可枚舉子集出發,可以有效地找出一個更大的遞歸可枚舉子集 。
相關結論
 創造集
創造集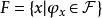 創造集
創造集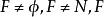 創造集
創造集定理1 設 為一元遞歸函式的集合, ,如果 是遞歸枚舉集,那么F是 創造集。
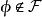 創造集
創造集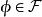 創造集
創造集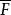 創造集
創造集證明:顯然空函式 ,因為不然的話F是生成集,與題設矛盾。因此 ,又由定理2,是生成集,從而F是創造集。證畢。
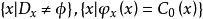 創造集
創造集運用本定理可以很快地判定 等遞歸枚舉集是創造集。
 創造集
創造集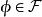 創造集
創造集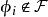 創造集
創造集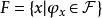 創造集
創造集定理2 設為一元遞歸函式的集合,,並且至少有一個,那么是生成集。
創造集的一個重要性質如下.
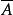 創造集
創造集定理3 如果A是創造集,那么A的補集 含有一個無窮的遞歸枚舉子集。
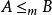 創造集
創造集定理4 設 ,若A是生產集,則B是生產集。
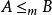 創造集
創造集推論 設 ,設A是創造集,B是遞歸可枚舉集,則B是創造集。
定理5 若A是單純集,那么A不是創造集 。

