定義
初等複變函數是實變數初等函式在複數域中的推廣。
初等函式
在實函式中，常數函式、冪函式、指數函式、對數函式、三角函式、反三角函式這六類函式稱為基本初等函式，而一切可由基本初等函式經過有限次四則運算和有限次複合生成的函式稱為初等函式。
復變數的初等函式
復變數的初等函式的定義形式上與初等函式相同，只不過它們的定義域已由實數集合推廣到複數域中。
性質
實變數的初等函式推廣到複數域後，在實數域中保持它們原有的性質，但在複數域中具有一些新的性質，如復變指數函式的周期性、復變對數函式的無窮多值性、復變正弦函式與復變餘弦函式的無界性等。
從這些新的性質可以看出，只有把這些函式從實數域推廣到複數域，才能更全面、更深刻地揭示它們的本質。
類型
復變根式函式
(radical function of a complex variable)
復變根式函式是實變數根式函式在複數域中的推廣。
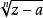初等複變函數形如，的函式稱為復變根式函式，其中n是大於 1的正整數，a是復常數。
復變指數函式
(exponent function of a complex variable)
復變指數函式是實變數指數函式在複數域中的推廣。
形如e =e =e (cos y+isin y)的函式稱為復變指數函式。
復變一般指數函式
(general exponent function of a complex variable)
復變一般指數函式是實變數一般指數函式在複數域中的推廣。
若a≠0，∞，則稱函式w=a =e log a為復變一般指數函式。
復變冪函式
(power function of a complex variable)
復變冪函式是實變數冪函式在複數域中的推廣。
形如w=z -e (z≠0，∞，a為復常數)的函式稱為復變冪函式。
復變對數函式
(logarithmic function of a tomplex variable)
復變對數函式是實變數對數函式在複數域中的推廣。
若e =z(z≠0，∞)，則複數w稱為複數z的對數，記為w=Logz=log|z|+i(arg z+2kπ)(k=0,±1,±2,...}。若限定-π<Im(Log z)≤π，則得到復變對數函式的主值（或主支），記為log z。
復變三角函式
(trigonometric functions of a complex variable)
復變三角函式是實變數三角函式在複數域中的推廣。
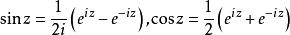初等複變函數復變正弦函式與餘弦函式定義為。當z為實數時，此定義與數學分析中關於正弦函式和餘弦函式的定義是一致的。
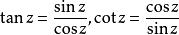初等複變函數復變正切函式與餘切函式定義為：。
復變反三角函式
(inverse trigonometric func- dons of a complex variable)
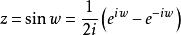初等複變函數
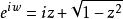初等複變函數
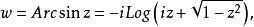初等複變函數
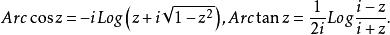初等複變函數復變反三角函式是實變數反三角函式在複數域中的推廣。由可解得由此定義復變反正弦函式為同樣地定義復變反餘弦函式和復變反正切函式為：
