歷史
切觸幾何的根源出現於克里斯蒂安·惠更斯、Barrow和牛頓的著作中。切觸變換的理論(也即保持一個切觸結構的變換)是索甫斯·李發展的,其目的是雙重的,包括研究微分方程(例如勒讓德變換)和表述射影對偶性中常見的'空間元素的變換。
定義
數學上,切觸幾何是研究奇數維流形上的完全不可積超平面的幾何。根據弗洛比尼斯定理,這個(大致來講)可以通過葉層結構的不成立來識別。作為它的姐妹,辛幾何屬於偶數維的世界,而切觸幾何是奇數維的對應幾何。
Reeb向量場
若α是一個給定切觸結構的切觸形式,Reeb向量場R可以定義維dα的核的唯一滿足α(R)=1的元素。其動力學可以用於研究切觸流形的結構甚或用諸如辛場論和嵌入切觸同調這類的Floer同調來研究流形本身。
形式和結構
一個切觸形式α在2 n+1維流形 M上就是一個(局部)1-流形,具有屬性
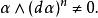 切觸幾何
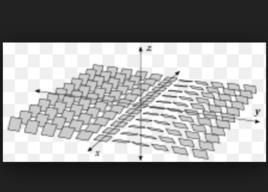
切觸幾何一個切觸結構ξ在一個流形上就是一個切觸形式α的核,也就是,一個完全不可積超平面場。大致來講,這表示你無法在一個開集上找到和ξ相切的一片超曲面。
從定義可以導出 dα限制到ξ上時是非退化的。這表示ξ是一個該流形上的辛叢。因為辛空間是偶數維的,切觸流形必須是奇數維的。
流形和紐結
切觸流形最有意思的子空間是它的勒讓德子流形。在(2n+1)-維流形上的切觸超平面場的不可積性意味著沒有2n-維子流形可以將它作為它的切叢,局部的都不行。但是,通常可以找到一個n-維(嵌入或者浸入)子流形,其切空間位於切觸場內。勒讓德子流形和辛流形的拉格朗日子流形類似。它們之間有一個精確的關係:勒讓德子流形在切觸流形的辛化中的提升是一個拉格朗日子流形。 勒讓德子流形的最簡單的例子是在一個切觸三維流形中的勒讓德紐結。不等價的勒讓德紐結可能作為光滑紐結是等價的。
勒讓德子流形是很剛性的對象;在一些情況下,子流形為了成為勒讓德子流形而必須解開紐結。辛場論提供勒稱為切觸同調的勒讓德子流形的不變數,它們有時可以用於區分拓撲等價的勒讓德子流形。
套用
切觸幾何和辛幾何一樣在物理學中有廣泛的套用,例如,幾何光學、經典力學、熱力學、幾何量子化、以及諸如控制論這樣的套用數學。它也可以用於證明有趣的事情,例如‘你總是可以平泊你的汽車,只要空間足夠大’。切觸幾何在低維拓撲中有很多套用;一個這種相關性的表現就是每個三維流形都有切觸結構。