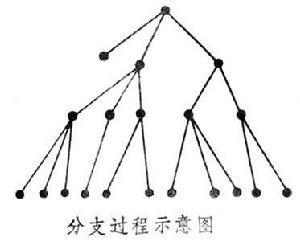
詳解
一種特殊的隨機過程,它是一組粒子的分裂或滅亡過程的數學模型。例如,某種生物群中,每一母體(粒子)生育第二代(或不生育),第二代中每一母體又生育第三代……。以Zn表示此群體中第n代的個體數,{Zn,n=0,1,2,…}便是一分支過程。又如,原子反應中的中子數也構成分支過程。以下設Z0=1,見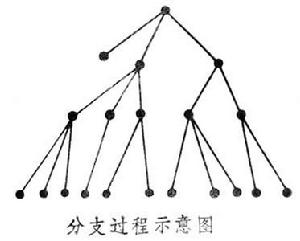 。
。 離散時間的分支過程 設時間參數為n=0,1,2,…,在分支過程理論中起重要作用的是分裂機率pk,它是任何一代的一個粒子分裂為 k個的機率(k=0,1,2,…)。其母函式(見機率分布)記為
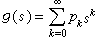 。假設各個粒子的分裂是獨立進行的,這種分支過程{Zn}通常稱為高爾頓-沃森過程(簡稱G-W過程),它是一個馬爾可夫鏈(見馬爾可夫過程)。
。假設各個粒子的分裂是獨立進行的,這種分支過程{Zn}通常稱為高爾頓-沃森過程(簡稱G-W過程),它是一個馬爾可夫鏈(見馬爾可夫過程)。 利用g(s)可求出有關{Zn}的下列諸量。若已知第n代的粒子數
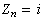 ,則下一代粒子數Zn+1=j的轉移機率為
,則下一代粒子數Zn+1=j的轉移機率為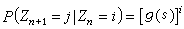 中sj的係數。以gn(s)表Zn的母函式:
中sj的係數。以gn(s)表Zn的母函式: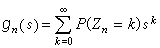 。由於Z0=1,g0(s)=s;
。由於Z0=1,g0(s)=s;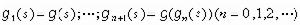 從而可求出
從而可求出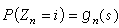 中si的係數。Zn的均值EZn=mn,其中m=EZ1=g┡(1)。
中si的係數。Zn的均值EZn=mn,其中m=EZ1=g┡(1)。 關於Zn的極限性質有:
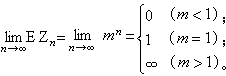
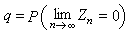 。可以證明q是方程g(s)=s (0≤s≤1)的最小根。又 q=1,若 m≤1;q<1,若 m>1,這時還有
。可以證明q是方程g(s)=s (0≤s≤1)的最小根。又 q=1,若 m≤1;q<1,若 m>1,這時還有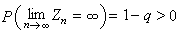 ,亦即粒子有無限增多的危險。
,亦即粒子有無限增多的危險。 G-W過程的一般化 設有m(≥2)種不同的粒子A1,A2,…Am,以
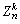 表第n代(或時刻n)的第k種粒子的個數,k=1,2,…,m,則
表第n代(或時刻n)的第k種粒子的個數,k=1,2,…,m,則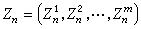 構成取值於m維格子點空間的馬爾可夫鏈。稱{Zn,n=0,1,2,…}為多種類G-W 過程。以
構成取值於m維格子點空間的馬爾可夫鏈。稱{Zn,n=0,1,2,…}為多種類G-W 過程。以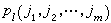 表Al中一個粒子分裂為Ak中jk個粒子(k=1,2,…,m)的機率。與上述g相仿,引進
表Al中一個粒子分裂為Ak中jk個粒子(k=1,2,…,m)的機率。與上述g相仿,引進 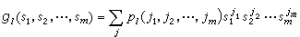 ,
,
 質細胞分支過程
質細胞分支過程連續時間分支過程 設時間參數 t≥0連續,b(t)Δt表示在短時間(t,t+Δt)中發生一次分裂的機率,pk(t)表示一個粒子分裂為k個的機率(k =0,1,2,…)。若b(t)、pk(t)連續,b(t)>0,
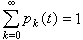 ,則在時刻t的粒子數Z(t)構成一連續時間馬爾可夫鏈,於是可利用後者的理論來研究{Z(t)}。若 b(t),pk(t)不依賴於t,則{Z(t)}是齊次的馬爾可夫鏈,這時可以得到許多類似於對 G-W 過程所得到的結果。
,則在時刻t的粒子數Z(t)構成一連續時間馬爾可夫鏈,於是可利用後者的理論來研究{Z(t)}。若 b(t),pk(t)不依賴於t,則{Z(t)}是齊次的馬爾可夫鏈,這時可以得到許多類似於對 G-W 過程所得到的結果。 參考書目
T. E.Harris,The Theory of Branching Processes,Springer-Verlag,Berlin,1965.K.B.Ashreya and P.E.Ney,Branching Processes,Springer-Verlag,Berlin,1972.
相關連線
分支過程的正則性http://www1.chkd.cnki.net/kns50/XSearch.aspx?KeyWord=%e5%88%86%e6%94%af%e8%bf%87%e7%a8%8b%e7%9a%84%e6%ad%a3%e5%88%99%e6%80%a7
具有擴散的分支過程http://www1.chkd.cnki.net/kns50/XSearch.aspx?KeyWord=%e5%85%b7%e6%9c%89%e6%89%a9%e6%95%a3%e7%9a%84%e5%88%86%e6%94%af%e8%bf%87%e7%a8%8b