全同態加密

同態加密是上世紀80年代提出來的一種能保護數據隱私的加密算法，2009年IBM的Craig Gentry首次提出了一種基於理想格的全同態算法。 如果一個算法能滿足： 1）加法同態 2）乘法同態 那么，我們稱之為全同態算法。

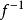同態加密

全同態加密

如果我們有一個加密函式 f , 把明文A變成密文A’, 把明文B變成密文B’，也就是說 f(A) = A’ ， f(B) = B’ 。另外我們還有一個解密函式，能夠將 f 加密後的密文解密成加密前的明文。

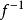全同態加密

對於一般的加密函式，如果我們將A’和B’相加，得到C’。我們用對C’進行解密得到的結果一般是毫無意義的亂碼。

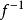全同態加密

但是，如果 f 是個可以進行同態加密的加密函式， 我們對C’使用進行解密得到結果C， 這時候的C = A + B。這樣， 數據處理權與數據所有權可以分離，這樣企業可以防止自身數據泄露的同時，利用雲服務的算力。

同態分類

a) 如果滿足f(A)+f(B)=f(A+B)， 我們將這種加密函式叫做加法同態
b) 如果滿足f(A)×f(B)=f(A×B)， 我們將這種加密函式叫做乘法同態。

如果一個加密函式 f只滿足 加法同態，就只能進行 加減法運算；

如果一個加密函式 f只滿足 乘法同態，就只能進行 乘除法運算;

如果一個加密函式同時滿足 加法同態和乘法同態，稱為 全同態加密。 那么這個使用這個加密函式完成各種加密後的運算(加減乘除、多項式求值、指數、對數、三角函式)。

第一個滿足加法和乘法同態的同態加密方法直到2009年才由Craig Gentry提出。

同態加密算法

RSA 算法對於乘法操作是同態的。

Paillier 算法則是對加法同態的。

Gentry算法則是全同態的。

1.

RSA 算法對於乘法操作是同態的。

2.

Paillier 算法則是對加法同態的。

3.

Gentry算法則是全同態的。